К вопросу о горизонте макроэкономического прогноза: новый взгляд на изменчивость рынков 1988-2004

Дмитриев Сергей Васильевич

Краснодар

Кубанский государственный технологический университет

Кафедра экономической теории

Постановка задачи "расчета" динамических свойств сложной экономической системы на любой интервал времени "прошлое-будущее" в вечном цикле "общего вида" относится к числу наисложнейших. На основе введенного автором суперпричинностного характера взаимосвязей в экономике получен макропрогноз на 15-летнем интервале времени "прошлое-настоящее-будущее". В определенной исходной метрике пространственноподобного интервала выделен временной дрейф системы, фазы и циклы, скорость обращения активов, метризация процессов переноса и перераспределения стоимости.

1. К истории вопроса о суперпричинности.

История вопроса восходит к 1917, 1935, 1960-80 годам и касается глубинных концептуальных процессов, вызванных существованием спонтанных процессов с определенным временем существования [1]. В свое время Эйнштейн подчеркнул, что слабость (квантовой) теории, заключается в том, что время и направление процесса представляются случайными. Здесь находятся истоки глубоких научных противоречий между Бором и Эйнштейном по поводу дополнительности и строгой причинности. В настоящее время известно, из опытов на эффекте Комптона, что причинность и закон сохранения выполняются в пределах ошибки эксперимента. Это область квантовой физики и общей теории относительности и нас в этом вопросе интересует только суперпричинность и проблемы детерминированности хаоса на рынках финансов и капиталов, связанные с областями несводимыми к материальной точке (точка-событие доходности), как это показано в наших работах [4].С точки зрения квантовой механики нет такого параметра, который позволял бы причинно увязать следствие "иррациональности" с каким - либо индивидуальным событием. Как известно, Эйнштейн предложил идею "поля-призрака или поле вероятности", которое "распространяется" в фазовом пространстве или т.н. конфигурационном пространстве. Квантовая механика дает следующее толкование этой идее: она применима к индивидуальным процессам, но принцип неопределенности накладывает ограничение и определяет тот "оптимальный вероятностный" объем информации, который можно получить из данного эксперимента или отображения для отдельного электрона (частицы). Проверка квантовомеханического предсказания требует, конечно, проведения многократного проведения эксперимента с "одиночной частицей" до тех пор, пока не будет получено с требуемой точностью распределение вероятности "в объеме". Еще десять лет тому назад такая задача относилась к классу "мысленных экспериментов", а в настоящее время в отдельных случаях она решается "итерациями приближения" на транспьютерах, когда возможно в процессе вычислений периодическое эмпирическое корректирование распределенной I/O информации.

Практически до конца своих дней Эйнштейн отстаивал свою точку зрения: понимание квантовых явлений отнюдь не требует отказа от классической причинности, - "то, что происходит в природе, по-видимому, настолько детерминировано, что глубокие закономерности связывают не только протекание процесса во времени, но и его начальное состояние. Я глубоко убежден в том, что мы- придем к сверхпричинности".

В понятие сверхпричиности он вкладывал единую теорию поля. Эйнштейн искал ее и его поиски, как известно, окончились неудачей. В нашей трактовке понятие сверхпричинности - это "счетные интервалы" времени возврата активов на рынках, которые содержат множество причинных траекторий порядка нескольких миллиардов точек (информационных переходов) в двумерном параметрическом фазовом пространстве, основанных на непрерывных структурах перераспределения стоимости.

Таким образом, новый подход к вопросам причинности и предсказумости на рынках финансов и капиталов сводится к обобщению закона стоимости и проистекающему из него принципа экономии рабочего времени. Закономерность суперпричинности в свою очередь определяет границы применимости принципа экономии и областей хаоса и упорядоченности в процессах самовозрастания капитала макросистемы, основанных на дискретных структурах переноса квантов стоимости в ПВ-многообразии.

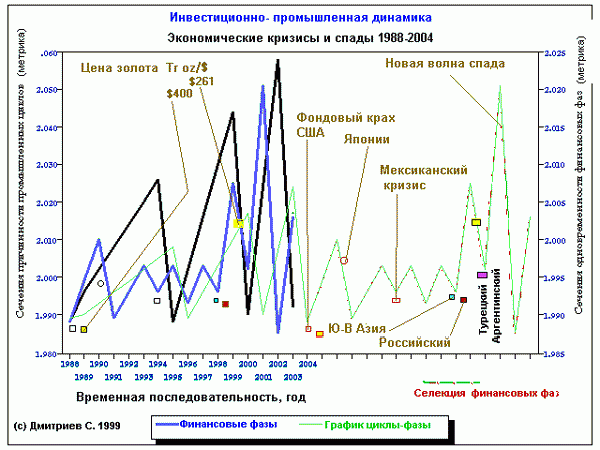
Рис.1. Макропрогноз " Прошлое-Настоящее- Будущее" на 15-летнем интервале общественно-необходимого времени формации. Для наглядности сделана селекция финансовых фаз ( сдвиг на 15 лет от 2004 г. )

2. Интервал необходимого времени: Прошлое - Настоящее - Будущее

Современная экономическая теория вступила в новейшую фазу своего развития [ 3].

Усложнение и глобализация экономических процессов выдвигает на передний план анализ темпоральных связей в единой "методологически универсальной комплексной системе", как обобщение закона стоимости, с топологически разделенными компонентами ПВ- многообразия [4 ]. В этом случае темпоральные связи выделенной временной компоненты и перенос стоимости в ПВ- интервале неопределенности точек-событий доходности в сферах обращения (инверсии) активов универсальной экономической формы сосредоточены в фазовых ячейках, несводимых к материальной точке. Тем самым фазовой ячейке в таком определении придается информационный характер с включением процессов "самоизмерений" перераспределения стоимости. Поскольку общественно-необходимое время содержит некоторое множество моментов времени UTC, то существенными являются лишь моменты переноса (перераспределения) стоимости, т.к. от этого зависит эволюция системы по относительному экономическому времени.

Исключительная сложность этих процессов проявляется в комплексном отображении "финитных причинных" подмножеств в бесконечномерном множестве на "нити" суперпричинности в пространстве Минковского как одномерное число равномерных конечномерных метризаций ПВ-многообразия. В содержательном смысле это "интервал" времени возврата активов на рынках или "фазовый портрет", который содержит множество причинных траекторий порядка нескольких миллиардов точек (информационных переходов) в двумерном параметрическом фазовом пространстве. "Траектории" этих комплекных отображений фрактальной структуры выглядят как прямые линии с резкими изломами в псевдоевклидовом пространстве, что указывает на нелинейность процессов.

Счетное конечномерное отображение подмножества неразличимых причинных интервалов "относительного времени" в бесконечномерном множестве суперпричинности наделяет "тяготением" ту область и в том временном интервале переноса стоимости, среди их множества, где норма эффективности инвестиций больше. Иначе, темп деградации производственных мощностей (и декапитализация), скорость обращения активов в системе, имеют глубокую внутреннюю взаимосвязь с фактором существующей квазипараллельности временного порядка UTC на мирохозяйственных рынках.

Необратимость в каждой из "нитей" суперпричинности пространстве Минковского оказывается связанной с необратимостью взаимодействия с нелокальным информационным окружением относительного времени.

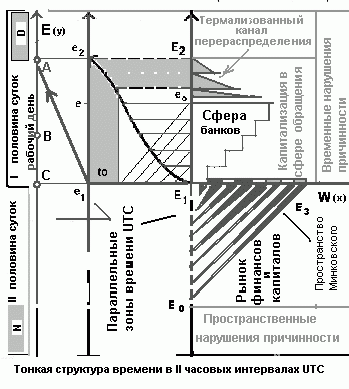
Рис.2. Тонкая структура параметрического ПВ многообразия в условиях комплиментарности хаоса и упорядоченности причинных подмножеств {UTC}.

{UTC}:{f(E(y));f(W(x))} многообразия универсальной экономической формы (экономии рабочего времени) в параллельных временных зонах UTC.

W(x), E(y) - параметрическая система координат ликвидность v доходность многообразия,

E1, e2, e1, A - суперпричинные связи в системе W(x), E(y).

E2, e2, - параллельные часовые зоны UTC (степени свободы фазового пространства ).

D, N - секторы нарушения причинности в половинах суток UTC.

Сфера банков - динамика ускорений доходности локальных ликвидных рынков, институтов чувствительных к малым возмущениям рынка.

E0 , E1, E3 - глобальные рынки финансов и капиталов непрерывного ценообразования в пространстве Минковского. Термализованный канал e1, A - направления переноса (отображение) особенностей одной системы (метрики) в другой (метрике) в процессах капитализации стоимости на локальном уровне, (цикл 1- 3 года) экономического времени.

Рекомендуем скачать другие рефераты по теме: решебник по математике 5, бесплатные рефераты.



1  2 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки