Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

ΔF = F(v1) · F(v1 + v).

В свою очередь, так как обе системы отсчета одинаковы, т.е. ни одна из систем не является преимущественной, а функция F(v1); F(v2) взаимодействий определяется одним и тем же законом. Предположим, что F(v) выглядит следующим образом для каждого из подпространств:

Рис. 1.

Но так как общее количество частиц принадлежащих каждому из подпространств стремится к бесконечности, то общее взаимодействие между обоими подпространствами будет определяться суммой всех взаимодействующих частиц и будет стремиться к

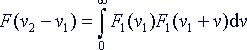
или учитывая, что (v2 – v1) = v

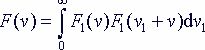
Полученное интегральное уравнение может иметь бесконечное количество решений, каждое из которых может быть привязано к определенным условиям.

В данном случае нами рассматривалось, что в какой бы системе мы ни находились и с какой бы скоростью не двигались относительно чего-либо, скорость распространения возмущения (света) везде будет определяться только условиями той системы в которой мы находимся, или производятся измерения, в частности плотностью материи ее температурой и т.д.

На этом, несколько незаконченном, общем подходе к материи как к бесконечной системе из которого возможно немного стало ясно независимость системы отсчета при определении конкретных величин, физического характера, мне кажется, следует закончить.

Что касается опытов Физо и Майкельсона, то оба эксперимента прежде всего доказывают независимость систем отсчета и в одинаковой степени могут служить, как для построения Теории относительности, так и любой другой, где будет соблюдаться принцип независимости систем отсчета.

Снова материя

В этой главе прежде всего пойдет речь об одном из возможных вариантов организации более мелких частиц материи в более крупные, при этом нам придется пользоваться теми немногими выводами произведенными ранее.

Таким образом, для построения возможной модели частицы материи, в нашем распоряжении имеется бесконечное пространство, заполненное бесконечным количеством частиц и существующее бесконечное количество времени, при этом в полученной таким образом среде может существовать сколько угодно больших или малых энергетических возмущений. Вполне очевидно, что в такой среде могут встречаться любые возможные объединения более мелких частиц в более крупные. Однако нас будут интересовать только устойчивые объединения, т.е. такие которые для одной из областей пространства будут удовлетворять третьему свойству материи. Поскольку проводить перебор всевозможных объединений практически невозможно, мы воспользуемся одной из известных моделей в Астрофизике под названием гравитационный коллапс. Однако, рассматривать явление коллапса мы будем несколько в другом плане.

Пускай в рассматриваемой среде в результате энергетических возмущений в некоторых точках пространства давление ниже, чем в остальных точках, тогда частицы материи из остальных точек пространства устремятся к образовавшейся таким образом области разряжения, при этом скорость которую приобретут частицы относительно друг друга будет определяться перепадом давлений и к центру разряжения. В тоже время необходимо учитывать, что в центре разряжения скорость распространения возмущений будет меньше, чем в открытом пространстве. Таким образом, встречные потоки частиц материи могут встречаться со скоростью большей скорости распространения возмущений (скорость света), однако как видно из предыдущих рассуждений о том, что взаимодействия между частицами уменьшаются по мере увеличения их относительной скорости и будет равно 0, при скорости равной или несколько большей скорости света. (Это вытекает также из Теории относительности – массы тел относительно друг друга будут мнимыми при их относительной скорости большей скорости света). Но в таком случае частицы материи двигающиеся к центру разряжения будут беспрепятственно покидать область разряжения не взаимодействуя с встречным потоком. Такая область, следовательно, может существовать устойчиво в пространстве достаточно большое время.

Подобное явление можно рассматривать как коллапс давления. Если не учитывать возможные завихрения возникающие при таком коллапсе, то скорость движения частиц можно определить исходя из уравнения движения используемого в гидроаэродинамике.

2W×v + grad (v 2/2) + ∂V/∂t = F – (1/ρ) grad p

для безвихревого движения: F = 0, 2W×v = 0, ∂v/∂t = 0

grad (v 2/2) = – (1/ρ) grad p.

Частный случай решения этого уравнения при ρ = const будет v=K/r2

В данном случае нами предполагается, что изменение давления может происходить за счет изменения таких характеристик среды, как температура без изменения ее плотности. Подобное динамическое объединение частиц материи можно рассматривать, как более крупную частицу материи. В дальнейшем если произвести рассмотрение подобной модели с учетом вихревых движений, то несложно будет получить модель галактик со всеми вытекающими физическими законами и явлениями действующими в последних, одновременно, это может быть и моделью атома. Однако для рассмотрения полных моделей необходимы более значительные затраты времени и поэтому в данном случае они рассматриваться не будут.

Исходя из полученных результатов, несложно определить размеры полученных гипотетических частиц материи для внешнего пространства в их трансформацию, в случае движения последних относительно данного пространства. Так если рассматривать скорость распространения возмущения как c – скорость света, то электрический радиус частиц материи будет равен. (В данном случае под электрическим подразумевается тот радиус частицы материи, который в какой-то мере определяет ее электрические взаимодействия, либо, как это будет показано далее, ядерные).

r0 = √(K/v), v = c, r0 = √(K/c)

для случая если частица неподвижна относительно выбранного пространства. Если частица движется относительно этого пространства, то с учетом сокращения Лоренца ее размеры будут иметь следующую зависимость от скорости движения относительно наблюдателя:

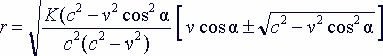
Рекомендуем скачать другие рефераты по теме: реферат слово, шпорі по философии.



Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки