Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Основной принцип проверки статистических гипотез можно сформули­ровать так: если наблюдаемое значение критерия принадлежит критичес­кой области - гипотезу отвергают, если наблюдаемое значение критерия принадлежит области принятия гипотезы -  гипотезу принимают.

Поскольку критерий К - одномерная случайная величина, все ее возможные значения принадлежат некоторому интервалу. Поэтому критическая область и область принятия гипотезы также являются интервалами, и, следовательно, существуют точки, которые их разделяют.

 Критическими точками Ккр называют точки, отделяющие критичес­кую область от области принятия гипотезы.

Различают, одностороннюю (правостороннюю или левостороннюю) и двустороннюю критические области.

Правосторонней называют критическую область, определяемую нера­венством К>Ккр , где  Ккр- положительное число.

Левосторонней называют критическую область, определяемую нера­венством КК1. 

1.6. Критерий Стьюдента

t-критерий Стьюдента применяется, когда необходимо сделать статистический вывод, равно ли математическое ожидание M{Х} генеральной совокупности некоторому предполагаемому значению С или ког­да требуется построить доверительный интервал для M{Х}. Обнаруже­но, что случайная величина t (при независимых наблюдениях) распреде­лена по закону Стьюдента, если Х распределена нормально:

где N- общее число наблюдений (объем выборки),

Х - среднее арифметическое случайной переменной Х;

S{Х),  S{X}- среднеквадратическое отклонение соответственно единичных значений Х и среднего арифметического Х.

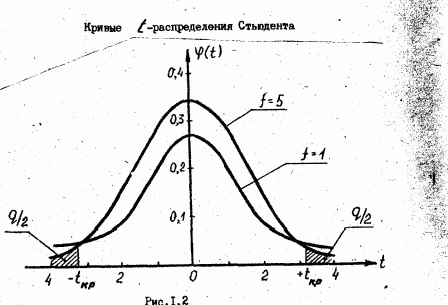
На рис.1.2 показаны кривые дифференциального закона распределе­ния Ф(t) для различных степеней свободы f=N-1 , по которым вычисляют несмещенную оценку дисперсии S2{ Х }   . При сравнитель­но небольших N кривая Ф(t) более пологая, чем нормальный закон распределения Ф(Х). При N-----  кривая Ф(t) приближается к кривой нормированного нормального распределения. Из рис.1.2 видно, что t-распределение симметрично относительно t=0, поэтому в таблицах, где даны критические значения tкр = tq,f  для принятого уровня значимости q и имеющегося чис­ла степеней свободы f , задаются только положительные tкр .

Если при расчете t по формуле (1.3) при подстановке в нее вместо М{X} предполагаемого значения С окажется, что t< tкр , то можно сделать вывод о том, что гипотеза М{X} = С    не проти­воречит результатам  наблюдения при принятой уровне значимости q .

В противном случае эта гипотеза отвергается с тем же уровнем значимости q. При этом остается возможность совер­шить ошибку первого рода, т.е. отвергнуть верную гипотезу с вероят­ностью q .                          -

Рассмотрим использование t-критерия Стьюдента для построения доверительного интервала для математического ожидания.

При t=tкр  разность [X - M{Х}] в (1.3) равна половине шири­ны доверительного интервала __  т.е.

Доверительный интервал, в котором с доверительной вероятностью P=I-q находится математическое ожидание M{X} , определяется следующими выражениями:

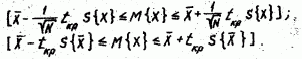
Поскольку мате­матическое ожидание М{X} есть истинное, объективно существующее неслучайное значение, а границы интервала - случайные величины (за счет наличия в них случайных величин X и S{X}), то правильно будет говорить о том, что доверительный интервал (1.5), (1.6) с ве­роятностью Р = I - q накрывает М {X}.

1.7. Критерий Фишера

Критерий Фишера применяется при проверке гипотезы о равенстве дисперсий двух генеральных совокупностей, распределенных по нормальному закону.

F-критерий Фишера называют дисперсионным отношением, так как он формируется как отношение двух сравниваемых несмещенных оценок дисперсий:

причем в числителе ставится большая из двух дисперсий. Расчетное F сравнивают с _____________, которое находят из таблиц, для степеней свободы  _____________________________________где N1 - число элементов выборки, по который вычислена _______ .

N2 - число элементов выборки, по которым получена оценка дисперсии ________.

Рекомендуем скачать другие рефераты по теме: ответы по тетради, реферат на английском языке.



Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки