
–ė—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł–Ķ –ľ–Ķ—ā–ĺ–ī–į —Ä–Ķ–Ņ–Ķ—Ä—ā—É–į—Ä–Ĺ—č—Ö —Ä–Ķ—ą–Ķ—ā–ĺ–ļ –≤ —Ü–Ķ–Ľ—Ź—Ö –ļ–ĺ—Ä—Ä–Ķ–ļ—Ü–ł–ł –Ņ—Ä–ĺ—Ą–Ķ—Ā—Ā–ł–ĺ–Ĺ–į–Ľ—Ć–Ĺ—č—Ö –ľ–ĺ—ā–ł–≤–ĺ–≤ —É —Ā—ā—É–ī–Ķ–Ĺ—ā–ĺ–≤ —ā–Ķ—Ö–Ĺ–ł—á–Ķ—Ā–ļ–ł—Ö –≤—É–∑–ĺ–≤
–ö–į—ā–Ķ–≥–ĺ—Ä–ł—Ź —Ä–Ķ—Ą–Ķ—Ä–į—ā–į: –†–Ķ—Ą–Ķ—Ä–į—ā—č –Ņ–ĺ —Ą–ł–∑–ļ—É–Ľ—Ć—ā—É—Ä–Ķ –ł —Ā–Ņ–ĺ—Ä—ā—É
–Ę–Ķ–≥–ł —Ä–Ķ—Ą–Ķ—Ä–į—ā–į: –Ī–Ķ—Ā–Ņ–Ľ–į—ā–Ĺ—č–Ķ —Ä–Ķ—ą–Ķ–Ī–Ĺ–ł–ļ–ł —Ā–ļ–į—á–į—ā—Ć, —Ä–Ķ—ą–Ķ–Ī–Ĺ–ł–ļ –Ņ–ĺ –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł–ł –į—ā–į–Ĺ–į—Ā—Ź–Ĺ
–Ē–ĺ–Ī–į–≤–ł–Ľ(–į) –Ĺ–į —Ā–į–Ļ—ā: Valuev.
–ü—Ä–Ķ–ī—č–ī—É—Č–į—Ź —Ā—ā—Ä–į–Ĺ–ł—Ü–į —Ä–Ķ—Ą–Ķ—Ä–į—ā–į | 1 2 3 4 5 | –°–Ľ–Ķ–ī—É—é—Č–į—Ź —Ā—ā—Ä–į–Ĺ–ł—Ü–į —Ä–Ķ—Ą–Ķ—Ä–į—ā–į
–í —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā–Ķ —ć—ā–ĺ–≥–ĺ –Ņ—Ä–ł –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–ľ —Ā–ĺ–Ņ–ĺ—Ā—ā–į–≤–Ľ–Ķ–Ĺ–ł–ł –ļ–į–∂–ī–ĺ–Ļ –Ņ–į—Ä—č –Ņ—Ä–ł–∑–Ĺ–į–ļ–ĺ–≤ –≤ —Ā—ā–ĺ–Ľ–Ī—Ü–į—Ö (–ł–Ľ–ł —Ā—ā—Ä–ĺ–ļ–į—Ö) —Ä–Ķ–Ņ–Ķ—Ä—ā—É–į—Ä–Ĺ–ĺ–Ļ —Ä–Ķ—ą–Ķ—ā–ļ–ł –Ņ—Ä–ĺ–ł—Ā—Ö–ĺ–ī–ł—ā –Ĺ–į–ļ–ĺ–Ņ–Ľ–Ķ–Ĺ–ł–Ķ —Ą–į–ļ—ā–ł—á–Ķ—Ā–ļ–ł—Ö —á–į—Ā—ā–ĺ—ā –į, –¨, —Ā, d.
–ě–Ī—Č–Ķ–Ķ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ –Ĺ–į–ļ–ĺ–Ņ–Ľ–Ķ–Ĺ–Ĺ—č—Ö —á–į—Ā—ā–ĺ—ā –≤ –ļ–į–∂–ī–ĺ–Ļ –Ņ–į—Ä–Ķ –ĺ–Ī—ä–Ķ–ļ—ā–ĺ–≤-—Ä–ĺ–Ľ–Ķ–Ļ –ł–Ľ–ł –ļ–ĺ–Ĺ—Ā—ā—Ä—É–ļ—ā–ĺ–≤ —Ä–į–≤–Ĺ–ĺ 20. –í—č—á–ł—Ā–Ľ–Ķ–Ĺ–ł—Ź –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī—Ź—ā—Ā—Ź –Ņ–ĺ —Ą–ĺ—Ä–ľ—É–Ľ–Ķ:
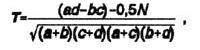
–≥–ī–Ķ –Ę - —ā–Ķ—ā—Ä–į—Ö–ĺ—Ä–ł—á–Ķ—Ā–ļ–ł–Ļ –ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā —Ā–ĺ–Ņ—Ä—Ź–∂–Ķ–Ĺ–Ĺ–ĺ—Ā—ā–ł –ß—É–Ņ—Ä–ĺ–≤–į;
N - —á–ł—Ā–Ľ–ĺ –≤–ĺ–∑–ľ–ĺ–∂–Ĺ—č—Ö –≤–į—Ä—Ć–ł—Ä—É–Ķ–ľ—č—Ö –Ņ—Ä–ł–∑–Ĺ–į–ļ–ĺ–≤ (–≤ –Ĺ–į—ą–Ķ–ľ —Ā–Ľ—É—á–į–Ķ —Ä–į–≤–Ĺ–ĺ 20);
–į, –¨, —Ā, d - —Ą–į–ļ—ā–ł—á–Ķ—Ā–ļ–ł–Ķ —á–į—Ā—ā–ĺ—ā—č.
–Ę–Ķ—ā—Ä–į—Ö–ĺ—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ –ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā—č –≤—č–ī–į—é—ā—Ā—Ź –≤ –≤–ł–ī–Ķ –ľ–į—ā—Ä–ł—Ü—č —Ā 20 —Ā—ā—Ä–ĺ–ļ–į–ľ–ł –ł 20 —Ā—ā–ĺ–Ľ–Ī—Ü–į–ľ–ł. –ó–Ĺ–į–ļ–ĺ–ľ (-) –ĺ–Ī–ĺ–∑–Ĺ–į—á–į—é—ā—Ā—Ź –ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā—č, –Ņ–ĺ–Ľ—É—á–ł–≤—ą–ł–Ķ—Ā—Ź –≤ —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā–Ķ —Ä–į–≤–Ķ–Ĺ—Ā—ā–≤–į –Ĺ—É–Ľ—é –ĺ–ī–Ĺ–ĺ–Ļ –ł–Ľ–ł –Ĺ–Ķ—Ā–ļ–ĺ–Ľ—Ć–ļ–ł—Ö —Ā–ļ–ĺ–Ī–ĺ–ļ –≤ —Ä–į—Ā—á–Ķ—ā–Ĺ–ĺ–Ļ —Ą–ĺ—Ä–ľ—É–Ľ–Ķ:
(–į+–¨)=0; (c+d)=0; (a+c)=0; (b+d)=0. –í –ī–į–Ĺ–Ĺ–ĺ–ľ —Ā–Ľ—É—á–į–Ķ –ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ –Ĺ–į 0 –ĺ–∑–Ĺ–į—á–į–Ķ—ā –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ –Ī–ĺ–Ľ—Ć—ą—É—é —Ā–≤—Ź–∑—Ć –ļ–ĺ–Ĺ—Ā—ā—Ä—É–ļ—ā–į (–ł–Ľ–ł —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į) —Ā –ĺ—Ā—ā–į–Ľ—Ć–Ĺ—č–ľ–ł.
–ó–Ĺ–į—á–ł–ľ–ĺ—Ā—ā—Ć —ā–Ķ—ā—Ä–į—Ö–ĺ—Ä–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā–į —Ā–ĺ–Ņ—Ä—Ź–∂–Ķ–Ĺ–Ĺ–ĺ—Ā—ā–ł –ĺ—Ü–Ķ–Ĺ–ł–≤–į–Ķ—ā—Ā—Ź –Ĺ–į –ī–ĺ–≤–Ķ—Ä–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ–ľ —É—Ä–ĺ–≤–Ĺ–Ķ –†=0,95 –Ņ–ĺ –ľ–Ķ—ā–ĺ–ī—É X2 (—Ö–ł-–ļ–≤–į–ī—Ä–į—ā).
X2=NT2;
–≥–ī–Ķ –Ę - —ā–Ķ—ā—Ä–į—Ö–ĺ—Ä–ł—á–Ķ—Ā–ļ–ł–Ļ –ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā —Ā–ĺ–Ņ—Ä—Ź–∂–Ķ–Ĺ–Ĺ–ĺ—Ā—ā–ł;
N - –ĺ–Ī—ä–Ķ–ľ –≤—č–Ī–ĺ—Ä–ļ–ł (–ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ –ļ–ĺ–Ĺ—Ā—ā—Ä—É–ļ—ā–ĺ–≤ –ł–Ľ–ł —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–ĺ–≤), N=20:
X2 - –ļ—Ä–ł—ā–Ķ—Ä–ł–Ļ –ĺ—Ü–Ķ–Ĺ–ļ–ł —Ā–ĺ–Ņ—Ä—Ź–∂–Ķ–Ĺ–Ĺ–ĺ—Ā—ā–ł –Ĺ–į–Ī–Ľ—é–ī–į–Ķ–ľ—č—Ö —Ą–į–ļ—ā–ĺ—Ä–ĺ–≤. –Ē–Ľ—Ź –Ĺ–į—ą–Ķ–≥–ĺ —Ā–Ľ—É—á–į—Ź –ĺ–Ĺ —Ä–į–≤–Ķ–Ĺ 3,841 [8].
–ü—Ä–ł –ł–∑—É—á–Ķ–Ĺ–ł–ł –Ņ—Ā–ł—Ö–ĺ–Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ —Ā–ľ—č—Ā–Ľ–į –≤–∑–į–ł–ľ–ĺ—Ā–≤—Ź–∑–ł –ļ–ĺ–Ĺ—Ā—ā—Ä—É–ļ—ā–ĺ–≤ (–ł–Ľ–ł —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–ĺ–≤) —Ą–į–ļ—ā —Ö–į—Ä–į–ļ—ā–Ķ—Ä–į —Ā–≤—Ź–∑–ł (–ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ –ł–Ľ–ł –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ) –ľ–Ķ–∂–ī—É –Ĺ–ł–ľ–ł –ł–ľ–Ķ–Ķ—ā –≤–į–∂–Ĺ–ĺ–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ. –ü–ĺ—ć—ā–ĺ–ľ—É —Ā –Ņ–ĺ–ľ–ĺ—Č—Ć—é —Ä–į—Ā—á–Ķ—ā–į –ĺ–∂–ł–ī–į–Ķ–ľ—č—Ö —á–į—Ā—ā–ĺ—ā –≤—č—á–ł—Ā–Ľ—Ź–Ľ–ĺ—Ā—Ć –Ĺ–į–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł–Ķ —Ā–≤—Ź–∑–ł ((+) –ł–Ľ–ł (-)).
![]()
–≥–ī–Ķ N - –ĺ–Ī—ä–Ķ–ľ –≤—č–Ī–ĺ—Ä–ļ–ł (–ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ –ļ–ĺ–Ĺ—Ā—ā—Ä—É–ļ—ā–ĺ–≤ –ł–Ľ–ł —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–ĺ–≤), N=20;
–į' - –ĺ–∂–ł–ī–į–Ķ–ľ–į—Ź —á–į—Ā—ā–ĺ—ā–į –≤ –ļ–Ľ–Ķ—ā–ļ–Ķ –į.
–ē—Ā–Ľ–ł –į > –į', —ā–ĺ —Ā–≤—Ź–∑—Ć –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ–į—Ź (+), –Ķ—Ā–Ľ–ł –į < –į', —ā–ĺ —Ā–≤—Ź–∑—Ć –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ–į—Ź (-).
–ó–Ĺ–į—á–ł–ľ—č–Ķ –ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā—č —Ā–ĺ–Ņ—Ä—Ź–∂–Ķ–Ĺ–Ĺ–ĺ—Ā—ā–ł –≤ –ľ–į—ā—Ä–ł—Ü–Ķ –ĺ—ā–ľ–Ķ—á–į—é—ā—Ā—Ź –∑–Ĺ–į–ļ–ĺ–ľ (*).
–§. –§—Ä–į–Ĺ—Ā–Ķ–Ľ–Ľ–į –ł –Ď. –Ď–į–Ĺ–Ĺ–ł—Ā—ā–Ķ—Ä [19] –Ņ—Ä–Ķ–ī–Ľ–į–≥–į—é—ā –ī–Ľ—Ź –į–Ĺ–į–Ľ–ł–∑–į —Ä–Ķ—ą–Ķ—ā–ļ–ł –Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į—ā—Ć—Ā—Ź –Ņ–ĺ–ļ–į–∑–į—ā–Ķ–Ľ–Ķ–ľ, –Ĺ–į–∑—č–≤–į–Ķ–ľ—č–ľ "–Ī–į–Ľ–Ľ–ĺ–ľ –≤–∑–į–ł–ľ–ĺ—Ā–≤—Ź–∑–ł*. –ü–ĺ—Ā–ļ–ĺ–Ľ—Ć–ļ—É —ā–Ķ—ā—Ä–į—Ö–ĺ—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ –ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā—č –≤–∑–į–ł–ľ–ĺ—Ā–≤—Ź–∑–ł –Ĺ–Ķ–Ľ–ł–Ĺ–Ķ–Ļ–Ĺ—č, –Ī–į–Ľ–Ľ –≤–∑–į–ł–ľ–ĺ—Ā–≤—Ź–∑–ł –Ľ–ĺ–≥–ł—á–Ĺ–ĺ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–ł—ā—Ć –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ—č–ľ —á–ł—Ā–Ľ–ĺ–ľ.
T1 = 100T2, –≥–ī–Ķ
T1 - –Ī–į–Ľ–Ľ –≤–∑–į–ł–ľ–ĺ—Ā–≤—Ź–∑–ł.
–Ę - —ā–Ķ—ā—Ä–į—Ö–ĺ—Ä–ł—á–Ķ—Ā–ļ–ł–Ļ –ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā.
–í–ĺ–∑–≤–Ķ–ī–Ķ–Ĺ–ł–Ķ –≤ –ļ–≤–į–ī—Ä–į—ā –ī–Ķ–Ľ–į–Ķ—ā –≤—Ā–Ķ —ā–Ķ—ā—Ä–į—Ö–ĺ—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ –ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā—č –≤–∑–į–ł–ľ–ĺ—Ā–≤—Ź–∑–ł –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ—č–ľ–ł. –£–ľ–Ĺ–ĺ–∂–Ķ–Ĺ–ł–Ķ –Ĺ–į 100 –ī–į–Ķ—ā –≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā—Ć –ł–∑–Ī–į–≤–ł—ā—Ć—Ā—Ź –ĺ—ā –ī—Ä–ĺ–Ī–Ķ–Ļ. –Ē–Ľ—Ź –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–ł—Ź –Ī–į–Ľ–Ľ–į –≤–∑–į–ł–ľ–ĺ—Ā–≤—Ź–∑–ł –Ľ—é–Ī–ĺ–≥–ĺ –ļ–ĺ–Ĺ—Ā—ā—Ä—É–ļ—ā–į —Ā—É–ľ–ľ–ł—Ä—É—é—ā—Ā—Ź –≤—Ā–Ķ –Ķ–≥–ĺ —ā–Ķ—ā—Ä–į—Ö–ĺ—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ –ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā—č –≤–∑–į–ł–ľ–ĺ—Ā–≤—Ź–∑–ł —Ā–ĺ –≤—Ā–Ķ–ľ–ł –ĺ—Ā—ā–į–Ľ—Ć–Ĺ—č–ľ–ł –ļ–ĺ–Ĺ—Ā—ā—Ä—É–ļ—ā–į–ľ–ł (–Ī–Ķ–∑ —É—á–Ķ—ā–į –∑–Ĺ–į–ļ–į). –í —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā–Ķ –Ņ–ĺ–Ľ—É—á–į–Ķ–ľ —á–ł—Ā–Ľ–ĺ–≤–ĺ–Ķ –≤—č—Ä–į–∂–Ķ–Ĺ–ł–Ķ –ĺ–Ī—Č–Ķ–Ļ –ī–ł—Ā–Ņ–Ķ—Ä—Ā–ł–ł, –ĺ–Ī—ä—Ź—Ā–Ĺ—Ź–Ķ–ľ–ĺ–Ļ –ī–į–Ĺ–Ĺ—č–ľ –ļ–ĺ–Ĺ—Ā—ā—Ä—É–ļ—ā–ĺ–ľ. –°–į–ľ—č–ľ –∑–Ĺ–į—á–ł–ľ—č–ľ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —ā–į–ļ–ĺ–Ļ –ļ–ĺ–Ĺ—Ā—ā—Ä—É–ļ—ā, –ļ–ĺ—ā–ĺ—Ä—č–Ļ –Ĺ–į–ł–Ī–ĺ–Ľ–Ķ–Ķ —ā–Ķ—Ā–Ĺ–ĺ —Ā–≤—Ź–∑–į–Ĺ —Ā–ĺ –≤—Ā–Ķ–ľ–ł –ļ–ĺ–Ĺ—Ā—ā—Ä—É–ļ—ā–į–ľ–ł —Ä–Ķ—ą–Ķ—ā–ļ–ł (–ł–ľ–Ķ–Ķ—ā –Ĺ–į–ł–Ī–ĺ–Ľ—Ć—ą–ł–Ļ –Ī–į–Ľ–Ľ –≤–∑–į–ł–ľ–ĺ—Ā–≤—Ź–∑–ł).
–Ē–Ľ—Ź –Ĺ–į–≥–Ľ—Ź–ī–Ĺ–ĺ–≥–ĺ –ĺ—ā–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł—Ź –≤–∑–į–ł–ľ–ĺ—Ā–≤—Ź–∑–ł –ļ–ĺ–Ĺ—Ā—ā—Ä—É–ļ—ā–ĺ–≤ (—ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–ĺ–≤) –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ –ľ–Ķ—ā–ĺ–ī –Ĺ–į–ł–Ī–ĺ–Ľ—Ć—ą–Ķ–≥–ĺ –ļ–ĺ—Ä—Ä–Ķ–Ľ—Ź—Ü–ł–ĺ–Ĺ–Ĺ–ĺ–≥–ĺ –Ņ—É—ā–ł –Ņ–ĺ –í—č—Ö–į–Ĺ–ī—É [5]. –Ē–Ľ—Ź –ļ–į–∂–ī–ĺ–≥–ĺ –ļ–ĺ–Ĺ—Ā—ā—Ä—É–ļ—ā–į (—ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į) –≤—č–Ī–ł—Ä–į–Ķ—ā—Ā—Ź –ļ–ĺ–Ĺ—Ā—ā—Ä—É–ļ—ā (—ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā), –ł–ľ–Ķ—é—Č–ł–Ļ –Ĺ–į–ł–Ī–ĺ–Ľ—Ć—ą–Ķ–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ —ā–Ķ—ā—Ä–į—Ö–ĺ—Ä–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā–į –≤–∑–į–ł–ľ–ĺ—Ā–≤—Ź–∑–ł (–Ī–Ķ–∑ —É—á–Ķ—ā–į –∑–Ĺ–į–ļ–į). –ē—Ā–Ľ–ł –Ĺ–Ķ—Ā–ļ–ĺ–Ľ—Ć–ļ–ĺ –ļ–ĺ–Ĺ—Ā—ā—Ä—É–ļ—ā–ĺ–≤ –ł–ľ–Ķ—é—ā –ĺ–ī–ł–Ĺ–į–ļ–ĺ–≤–ĺ –Ĺ–į–ł–Ī–ĺ–Ľ—Ć—ą—É—é –≤–∑–į–ł–ľ–ĺ—Ā–≤—Ź–∑—Ć, —ā–ĺ —É—á–ł—ā—č–≤–į—é—ā—Ā—Ź –≤—Ā–Ķ —ć—ā–ł –ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā—č.
–†–Ķ–ļ–ĺ–ľ–Ķ–Ĺ–ī—É–Ķ–ľ —Ā–ļ–į—á–į—ā—Ć –ī—Ä—É–≥–ł–Ķ —Ä–Ķ—Ą–Ķ—Ä–į—ā—č –Ņ–ĺ —ā–Ķ–ľ–Ķ: —ą–Ņ–į—Ä–≥–į–Ľ–ļ–ł –Ņ–ĺ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–Ķ, bestreferat.
–ü—Ä–Ķ–ī—č–ī—É—Č–į—Ź —Ā—ā—Ä–į–Ĺ–ł—Ü–į —Ä–Ķ—Ą–Ķ—Ä–į—ā–į | 1 2 3 4 5 | –°–Ľ–Ķ–ī—É—é—Č–į—Ź —Ā—ā—Ä–į–Ĺ–ł—Ü–į —Ä–Ķ—Ą–Ķ—Ä–į—ā–į