Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

 (3)

 (4)

 (5)

, (6)

где:

εi, σi— деформации и нормальные напряжения вдоль i-й оси, i=1,2,3;

ij, ij — деформации сдвига и касательные напряжения в соответствующих плоскостях;

— модуль сдвига для плоскости изотропии.

Для определения упругих констант каждый образец испытывался по трем программам нагружения. Задавая значения приращений напряжений Δσ и измеряя соответствующие приращения деформаций Δεi , были определены значения упругих модулей Е, Е', v и v'.

Испытания показали, что модули упругости Е' вдоль вертикальной оси для всех образцов примерно в полтора раза ниже, чем модули упругости Е в горизонтальной плоскости, и составляют примерно 1,5-2.105 атм., а коэффициенты Пуассона примерно одинаковы и равны 0,14-0,20.

Более подробно методики измерения скоростей продольных волн в породе и определения ее упругих характеристик будут описаны в статье в одном из следующих номеров журнала.

Что касается пятой упругой константы — модуля G', то для его определения необходимо иметь возможность выпилить образец под углом 45° к оси изотропии, т.е. к оси скважины. Керн диаметром 80 мм, предоставленный для проведения исследований, не позволял этого сделать. Но поскольку величина G' необходима для расчетов, то для ее задания были использованы результаты, приведенные в [1]. В ней собраны численные значения всех технических упругих констант для 47 различных горных пород (алевролиты, песчаники, известняки, сланцы и т.д.). Численные значения констант взяты из экспериментальных исследований разных авторов. Анализ этих данных позволил сделать следующий вывод. Хотя модуль G' является независимой константой, для 45 пород (из 47) можно указать приближенную формулу, связывающую G' с остальными упругими константами:

. (7)

Поэтому в дальнейшем мы будем пользоваться значениями G', полученными из этой формулы.

Программы испытаний образцов

Одним из основных достоинств испытательного стенда ИСТНН является возможность воссоздания на нем истинных напряженных состояний, возникающих в породе в окрестности скважины, вблизи перфорационных отверстий, щелей и т.д., на любой стадии бурения, освоения и работы скважины.

Это в полной мере относится и к ГС, бурящимся в пластах с ярко выраженной анизотропией деформационных свойств породы. Однако подход к моделированию напряженно-деформированных состояний, возникающих вокруг ГС в трансверсально-изотропном пласте, значительно отличается от того, который обычно применяется для случая вертикальных скважин. Это связано с тем, что в случае вертикальной скважины все точки на ее контуре абсолютно идентичны с точки зрения действующих в них напряжений как для изотропного, так и для трансверсально-изотропного пласта. В горизонтальной же скважине дело обстоит иначе. Если в случае изотропного пласта действующие напряжения также постоянны по контуру скважины, то при наличии анизотропии напряжения существенно меняются по контуру скважины и зависят от упругих характеристик породы.

На рис. 1 схематично показано сечение горизонтальной не обсаженной скважины и действующие на стенках скважины радиальное σR и кольцевое σθ напряжения в двух точках M и N.

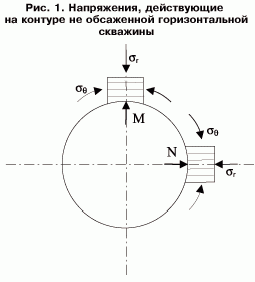
Радиальные напряжения σR во всех точках по контуру скважины одинаковы и равны давлению жидкости в скважине. Кольцевые же напряжения σθ будут меняться от точки к точке.

На рис. 2 показано распределение кольцевых напряжений σθ вокруг горизонтальной скважины в трансверсально-изотропной среде, ось скважины параллельно плоскости изотропии [1]. При расчетах в соответствии с измеренными значениями модулей упругости образцов породы в вертикальном и горизонтальном направлениях полагалось, что модуль упругости породы в вертикальном направлении в 1,5 раза меньше модуля упругости в горизонтальном направлении. В качестве единицы на рис. 2 принята разность между величиной горного давления на данной глубине и значением давления жидкости в скважине. Изображенная на рис. 2 окружность представляет собой кольцевые напряжения σθ, которые бы действовали в окрестности горизонтальной скважины, если бы пласт был изотропным. Из рис. 2 видно, что максимальные кольцевые напряжения σθ действуют в точках M и N. Поэтому максимальные касательные напряжения, действующие в окрестности скважины и равные (σθ-σR)/2, также будут наибольшими в этих точках.

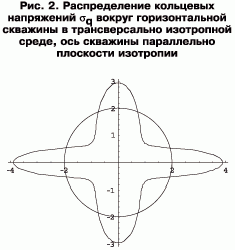
Поскольку разрушение породы происходит за счет действия касательных напряжений, на установке ИСТНН моделировались напряженные состояния именно в точках M и N, как наиболее опасных с точки зрения разрушения ствола скважины. Основное отличие при испытаниях образцов для точек M и N состояло в том, что в точке N напряжения σθ действуют перпендикулярно плоскости напластования, а в точке M — параллельно ей. Соответственно должны располагаться в нагружающем узле ИСТНН и образцы породы во время испытаний.

При уменьшении давления жидкости в скважине радиальные напряжения σR в точках M и N, равные давлению жидкости, будут также уменьшаться, а кольцевые напряжения σθ будут расти, поскольку они пропорциональны разности между величиной горного давления и значением давления жидкости в скважине.

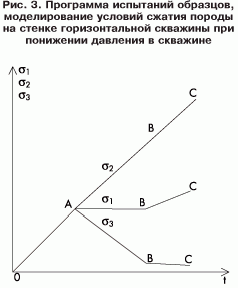
Соответствующая программа испытаний показана на рис. 3. Изображенные на нем напряжения (σ1, σ2, σ3 относятся к осям нагружающего узла ИСТНН, в которых по оси 2 напряжение всегда возрастает, т.е. напряжение σ2 является так называемым параметром нагружения. Применительно к осям скважины напряжение σ2 отвечает напряжению σθ.

Рекомендуем скачать другие рефераты по теме: доклади по биологии, контрольная работа за полугодие.



Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки