Предыдущая страница реферата | 1  2  3  4

Граничные условия для ГТС

Как следует из постановки задачи выше, граничными условиями являются либо задание распределения расхода газа по времени на КС Q(t), либо задание P(t) или Q(t) на подкачках и отборах. Так как для подкачек и отборов задается либо давление, либо расход, то оставшееся неизвестное необходимо определять на каждом временном слое.

Представим, что на одном конце трубы задано P(t), а на другом Q(t). Если мы знаем на каждом временном слое Q(t) для подкачки или отбора, то давление вычисляется по обычной схеме (рис.3). Для P(t) дело обстоит несколько сложнее. На рис.7 рассмотрены оба таких примера.

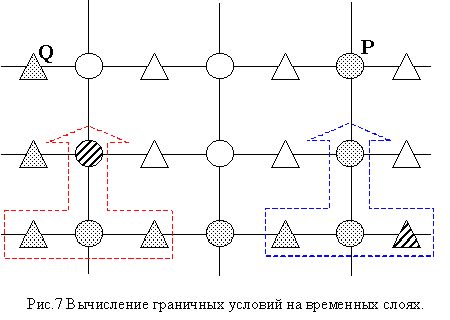
Из рис.7 следует, что неизвестный расход определяется по известному давлению на следующем временном слое, давлению и расходу текущего слоя.

Заключение

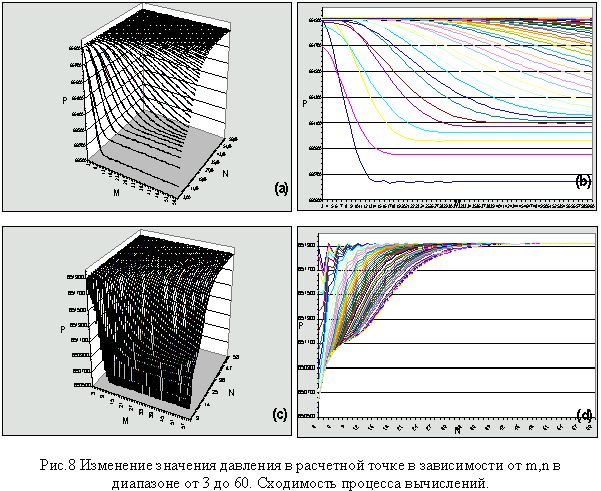
Для доказательства сходимости процесса вычислений по приведенной выше математической модели ГТС были проведены следующие эксперименты. Для трубы с фиксированными физическими параметрами и заданным начальным состоянием по давлению (стационарное течение газа между концами трубы ) наблюдалось выравнивание давления в замкнутом пространстве, то есть при условии, что оба конца трубы закрыты. Каждый эксперимент заключался в изменении числа n (кол-во узлов вдоль трубы на текущий промежуток времени) и числа m (кол-во узлов по времени в определенной точке трубы). В результате была получена сетка m x n значений давления в точке плоскости пространства и времени. На рис.8 значения m и n изменялись в диапазоне 3,....,60. Разброс значений давления P для исследуемой точки (3000сек. на 50м) в полученной сетке максимально равен 1300 Н/м2  (абсолютная погрешность), что составляет около 2% (относительная погрешность) от среднего значения давления в этой точке.

Исследование данной сетки привело к следующим выводам:

Увеличение числа m слабо влияет на увеличение точности вычислений при n>30. В этом случае относительная погрешность составила менее 1% Хотя при 3<n<30 относительная погрешность может достигнуть до 2%.

Увеличение числа n значительно сказывается на относительной погрешности только при m>13 (рис.8b). Однако рекомендуется использовать n>30, т.к. при этом давление в точке равномерно без скачков стремится к своему предельному значению (рис.8d). Природа колебания значения давления около определенной кривой объясняется апроксимацией значения давления разностной схемой решения на грубых сетках. Поэтому лучше использовать n>30, но при этом значительно увеличивать n не имеет смысла., так как увеличится время расчетов.

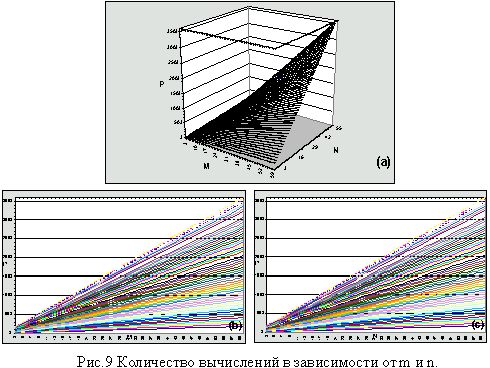
Необходимо отметить изменение количества вычислений в зависимости от n и m, то есть трудоемкость вычислительного процесса. На рис.9(a-d) представлена поверхность изменения количества вычислений. На ее основе и используя результаты исследований (рис.8) можно сделать вывод об оптимальном сочетании качества и количества вычислений для трубы. Наиболее оптимальными являются значения n=30, m=30 или около этого диапазона. Хотя, конечно, для детализации процесса по времени можно увеличивать значение m, но существенного улучшения относительной погрешности это не даст. Ее изменение составит не более 1%.

http://www.laboratory.ru/articl/math/ram01a.htm

http://www.laboratory.ru/articl/math/ram01b.htm

Список литературы

Сергованцев В.Т., Кучин Б.Л., Гарляускас А.И., и др. Централизованный контроль и оптимальное управление на магистральных газопроводах. vЛ.: Недра, 1973.

Карманов В.Г. Математическое программирование. vМ.: Наука, 1975.

Фильчиков П.Ф. Справочник по высшей математике. vКиев: Наукова думка, 1974.

Мантуров О.В. Курс высшей математики. vМ.: Высшая школа, 1991

Дьяконов В.П. Справочник по алгоритмам и программам на языке Бейсик для персональных ЭВМ. vМ.: Наука, 1987.

Новоселов В.Ф., Гольянов А.И., Муфтахов Е.М. Типовые расчеты при проектировании и эксплуатации газопроводов. vМ.: Недра, 1982.

Бобровский С.А., Щербаков С.Г., Гусейн-Заде М.А. Движение газа в газопроводах с путевым отбором. vМ.: Наука, 1972.

Березина И.В. Ретинский В.С. Оперативное управление системами газоснабжения.

Круг А.Г., Сосоулин Ю.А., Фатуев В.А. Планирование эксперимента в задачах идентификации и экстраполяции. vМ.: Наука, 1977.

Боглаев Ю.П. Вычислительная математика и программирование. vМ.: Высшая школа, 1990.

Скачали данный реферат: Кравченко, Chervjachok, Тупицын, Жестакова, Толбанов, Ярошинский, Tolstoj.
Последние просмотренные рефераты на тему: рассказы, шпаргалки по гражданскому праву, ответы 5 класс, реферати безкоштовно.



Предыдущая страница реферата | 1  2  3  4

Поделитесь этой записью или добавьте в закладки