Рефераты | Рефераты по географии | Построение геологической модели и прогнозного разреза | страница реферата 3 | Большая Энциклопедия Рефератов от А до Я
Большая Энциклопедия Рефератов от А до Я
  • Рефераты, курсовые, шпаргалки, сочинения, изложения
  • Дипломы, диссертации, решебники, рассказы, тезисы
  • Конспекты, отчеты, доклады, контрольные работы


    • Рефераты | Рефераты по географии | Построение геологической модели и прогнозного разреза


    Рефераты | Рефераты по географии | Построение геологической модели и прогнозного разреза

    Построение геологической модели и прогнозного разреза




    Категория реферата: Рефераты по географии
    Теги реферата: реферат народы, антикризисное управление предприятием
    Добавил(а) на сайт: Белкин.



    Предыдущая страница реферата | 1  2  3  4  5 |



    (азимут с учетом перехода через нуль)

    Dz = Dl*cos(Рефераты | Рефераты по географии | Построение геологической модели и прогнозного разреза)

    Балансный тангенциальный метод - исследуемый участок ствола скважины между двумя точками замера разбивается на два участка одинаковой длины: верхний и нижний. Каждый участок интерполируется отрезком прямой, причем зенитный угол и азимут прямой, интерполирующей верхний участок, принимаются равными соответствующим углам в верхней точке замера, а зенитный угол и азимут прямой, интерполирующей нижний участок, принимаются равными соответствующим углам в нижней точке замера. Приращения координат:

    Dx = Рефераты | Рефераты по географии | Построение геологической модели и прогнозного разреза,

    Dy = Рефераты | Рефераты по географии | Построение геологической модели и прогнозного разреза,

    Dz = Рефераты | Рефераты по географии | Построение геологической модели и прогнозного разреза.

    Метод кольцевых дуг - исследуемый участок ствола скважины между двумя точками замера представляется как дуга окружности. Каждая дуга лежит на наклонной плоскости, положение которой определяется по известным зенитным углам и азимутам в точках замера. Дуги проводятся таким образом, чтобы касательные вектора в точках замера были касательными к проводимым дугам. Радиус дуги определяется из условия, что длина дуги должна быть такой же, как измеренное по стволу скважины расстояние между точками замера.

    Метод, основанный на предположении о линейном изменении параметров (метод трапеций) - предполагается, что на исследуемом участке траектории ствола скважины азимут и зенитный угол изменяются линейно:

    Рефераты | Рефераты по географии | Построение геологической модели и прогнозного разреза, где Рефераты | Рефераты по географии | Построение геологической модели и прогнозного разреза, Рефераты | Рефераты по географии | Построение геологической модели и прогнозного разреза, где Рефераты | Рефераты по географии | Построение геологической модели и прогнозного разреза,

    тогда приращения координат:

    Dx = Рефераты | Рефераты по географии | Построение геологической модели и прогнозного разреза 

    Dy = Рефераты | Рефераты по географии | Построение геологической модели и прогнозного разреза Dz = Рефераты | Рефераты по географии | Построение геологической модели и прогнозного разреза

    Для проверки и сравнения этих методов они были опробованы на модельных скважинах. Траектория скважины задавалась параметрическими уравнениями вида: x = x(t), y = y(t), z = z(t). Касательный вектор Рефераты | Рефераты по географии | Построение геологической модели и прогнозного разреза к траектории скважины в точке соответствующей параметру t = t0 – (x¢(t0),y¢(t0), z¢(t0)). Зная его можно найти значения азимута и зенита в данной точке.

    для 1й четверти (для остальных аналогично)

    Рефераты | Рефераты по географии | Построение геологической модели и прогнозного разрезаАзимут=arcsin(Рефераты | Рефераты по географии | Построение геологической модели и прогнозного разреза)

    Рефераты | Рефераты по географии | Построение геологической модели и прогнозного разреза


    Рефераты | Рефераты по географии | Построение геологической модели и прогнозного разреза

    Рефераты | Рефераты по географии | Построение геологической модели и прогнозного разрезаРефераты | Рефераты по географии | Построение геологической модели и прогнозного разрезаРефераты | Рефераты по географии | Построение геологической модели и прогнозного разрезаРефераты | Рефераты по географии | Построение геологической модели и прогнозного разрезаРефераты | Рефераты по географии | Построение геологической модели и прогнозного разреза
    Зенит=arctg(Рефераты | Рефераты по географии | Построение геологической модели и прогнозного разреза)

    Глубина по стволу l, соответствующая параметру t=t0: l=Рефераты | Рефераты по географии | Построение геологической модели и прогнозного разреза,

    (константа интегрирования находится из условия l=0 при t=начальному значению). Найденные таким образом тройки значений Глубина, Азимут, Зенит – использовались в качестве исходных данных для проверяемых методов, результаты, работы которых сравнивались со значениями полученными из уравнения траектории скважины.

    Ниже указаны три наиболее характерные модели и результаты, полученные на них.

    №

    Уравнения

    Глубина по стволу

    .


    Рекомендуем скачать другие рефераты по теме: конспект 6 класс, м реферат.



    Предыдущая страница реферата | 1  2  3  4  5 |




    Поделитесь этой записью или добавьте в закладки

       

    Категории:



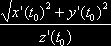    Разделы сайта




    •