Рефераты | Рефераты по информатике, программированию | Двоичные деревья поиска Двоичные деревья поиска Категория реферата: Рефераты по информатике, программированию Теги реферата: отчет о прохождении практики, шпоры на экзамен Добавил(а) на сайт: Dvoreckov. Предыдущая страница реферата | 13  14  15  16  17  18  19  20  21  22  23 | Следующая страница реферата 68   node.color = BLACK; 69 End

Процедура RBTDeleteFixUp применяется к дереву, которое обладает свойствами КЧД, если учесть дополнительную единицу черноты в вершине node (она теперь дважды чёрная, это чисто логическое понятие, и оно нигде фактически не сохраняется и логического типа для хранения цвета вам всегда будет достаточно) и превращает его в настоящее КЧД.

Что такое дважды чёрная вершина? Это определение может запутать. Формально вершина называется дважды чёрной, дабы отразить тот факт, что при подсчёте чёрных вершин на пути от корня до листа эта вершина считается за две черных. Если чёрная вершина была удалена, её черноту так просто выкидывать нельзя. Она на счету. Поэтому временно черноту удалённой вершины передали вершине node. В задачу процедуры RBTDeleteFixUp входит распределение этой лишней черноты. Они или будет передана красной вершине (и та станет чёрной) или после перестановок других чёрных вершин (дабы изменить их количество на пути от корня к листьям) будет просто выкинута.

В цикле (строки 3-67) дерево изменяется, и значение переменной node тоже изменяется, но сформулированное свойство остаётся верным. Цикл завершается, если:

node указывает на красную вершину, тогда мы красим её в чёрный цвет (строка 68).

node указывает на корень дерева, тогда лишняя чернота может быть просто удалена.

Могло оказаться, что внутри тела цикла удается выполнить несколько вращений и перекрасить несколько вершин, так что дважды чёрная вершина исчезает. В этом случае присваивание node = Tree.root (строки 33 и 64) позволяет выйти из цикла.

Внутри цикла node указывает на дважды чёрную вершину, а nodeTemp – на её брата (другую вершину с тем же родителем). Поскольку вершина node дважды чёрная, nodeTemp не может быть NIL, поскольку в этом случае вдоль одного пути от node.nodeParent было бы больше чёрных вершин, чем вдоль другого. Четыре возможных случая показаны на рисунке ниже. Зелёным и синим, помечены вершины, цвет которых не играет роли, то есть может быть как черным, так и красным, но сохраняется в процессе преобразований.

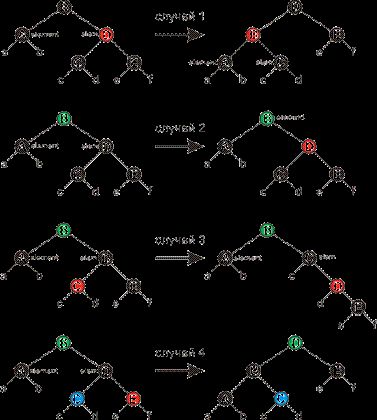
Рисунок 8

Убедитесь, что преобразования не нарушают свойство 4 КЧД (помните, что вершина node считается за две чёрные, и что в поддеревьях a - f изначально не равное количество чёрных вершин).

Случай 1 (строки 9-14 и 40-45) имеет место, когда вершина nodeTemp красная (в этом случае node.nodeParent чёрная). Так как оба потомка вершины nodeTemp чёрные мы можем поменять цвета nodeTemp и node.nodeParent и произвести левое вращение вокруг node.nodeParent не нарушая свойств КЧД. Вершина node остается дважды чёрной, а её новый брат – чёрным, так что мы свели дело к одному из случаев 2-4.

Случай 2 (строки 16-19 и 47-50). Вершина nodeTemp – чёрная, и оба её потомка тоже чёрные. В этом случае мы можем снять лишнюю чёрноту с node (теперь она единожды чёрная), перекрасить nodeTemp, сделав ёё красной (оба её потомка чёрные, так что это допустимо) и добавить черноту родителю node. Заметим, что если мы попали в случай 2 из случая 1, то вершина node.nodeParent – красная. Сделав её чёрной (добавление чёрного к красной вершине делает её чёрной), мы завершим цикл.

Случай 3 (строки 23 – 28 и 53 - 59) Вершина nodeTemp чёрная, её левый потомок красный, а правый чёрный. Мы можем поменять цвета nodeTemp и её левого потомка и потом применить правое вращение так, что свойства КЧД будут сохранены. Новым братом node будет теперь чёрная вершина с красным правым потомком, и случай 3 сводится к случаю четыре.

Случай 4 (строки 29 – 33 и 60 - 64) Вершина nodeTemp чёрная, правый потомок красный. Меняя некоторые цвета (не все из них нам известны, но это нам не мешает) и, производя левое вращение вокруг node.nodeParent, мы можем удалить лишнюю черноту у node, не нарушая свойств КЧД. присваивание node = Tree.root выводит нас из цикла.

Сравнительные характеристики скорости работы различных структур данных

Чтобы всё сказанное до этого не казалось пустой болтовнёй, я в качестве заключения приведу сравнительные характеристики скорости работы различных структур данных (деревьев и массивов). Для измерения времени была использована функция WinAPI QueryPerfomanceCounter. Время пересчитано в микросекунды. В скобках приведена конечная глубина дерева. Тестирование проводилось на процессоре Intel Celeron Tualatin 1000MHz с 384Мб оперативной памяти. В качестве ключа использовалось число типа int (32-х битное целое со знаком), а в качестве данных число типа float (4-х байтное вещественное).

Главная | Партнеры | Лучшие рефераты

Обратная связь

Рефераты | Рефераты по информатике, программированию | Двоичные деревья поиска | страница реферата 18 | Большая Энциклопедия Рефератов от А до Я    Все рефераты, курсовые, дипломы, шпаргалки, сочинения, изложения, решебники, конспекты являются общедоступными    Копирование и размещение в интернете разрешается только при наличии активной индексируемой ссылки на Ahaha.ru

© 2006-2020 «Ahaha.ru»