Рефераты | Рефераты по информатике, программированию | Двоичные деревья поиска
Двоичные деревья поискаКатегория реферата: Рефераты по информатике, программированию Теги реферата: отчет о прохождении практики, шпоры на экзамен Добавил(а) на сайт: Dvoreckov. Предыдущая страница реферата | 4 5 6 7 8 9 10 11 12 13 14 | Следующая страница реферата int data; protected: static CTreeBase<CTree> treeNil; }; //////////////////////////////////////////////////////////// CTreeBase<CTree> CTree::treeNil(&treeNil, &treeNil, &treeNil); |
Теперь везде в классе CTree можно использовать переменную treeNil. Преимущества очевидны. Потратив каких-то двенадцать (3 * sizeof(CTree *)) байт памяти, мы упростили разработку и ускорили выполнение программы.
Основной проблемой использования ДДП является то, что методы вставки и удаления вершин, гарантируя сохранение свойства упорядоченности, совершенно не способствуют оптимизации основных операций над ДДП. Например, если вставить в ДДП последовательность возрастающих или убывающих чисел, оно превратится, по сути, в двусвязный список, а основные операции будут занимать время, пропорциональное количеству вершин, а не его логарифму.
Таким образом, для получения производительности порядка O(log2N) нужно, чтобы дерево имело как можно более высокую сбалансированность (то есть имело возможно меньшую высоту). Обычно выделяются несколько типов сбалансированности. Полная сбалансированность, это когда для каждой вершины дерева количества вершин в левом и правом поддеревьях различаются не более чем на 1. К сожалению, такой сбалансированности трудно добиться на практике. Поэтому на практике используются менее жесткие виды сбалансированности. Например, русскими математиками Г. М. Адельсон-Вельским и Е.М.Ландисом были разработаны принципы АВЛ деревьев. В АВЛ деревьях для каждой вершины дерева глубины обоих поддеревьев различаются не более чем на 1. Еще одним “продвинутым” видом деревьев является так называемые красно-чёрные деревья. АВЛ деревья обеспечивают более высокую сбалансированность дерева, но затраты на их поддержание выше. Поскольку на практике разница в сбалансированности между этими двумя видами деревьев не высока, чаще используются красно-чёрные деревья.
Красно-чёрные деревья (Red-Black Tree, RB-Tree)
Итак, одним из способов решения основной проблемы использования ДДП являются красно-чёрные деревья. Красно-чёрные (название исторически связано с игральными картами, поскольку из них легко делать простые модели) деревья (КЧД) – это ДДП, каждая вершина которых хранит ещё одно дополнительное логическое поле (color), обозначающее цвет: красный или чёрный. Фактически, в КЧД гарантируется, что уровни любых двух листьев отличаются не более, чем в два раза. Этого условия оказывается достаточно, чтобы обеспечить скоростные характеристики поиска, близкие к O(log2N). При вставке/замене производятся дополнительные действия по балансировке дерева, которые не могут не замедлить работу с деревом. При описании алгоритмов мы будем считать, что NIL – это указатель на фиктивную вершину, и операции (NIL).left, (NIL).right, (NIL).color имеют смысл. Мы также будем полагать, что каждая вершина имеет двух потомков, и лишь NIL не имеет потомков. Таким образом, каждая вершина становится внутренней (имеющей потомков, пусть и фиктивных), а листьями будут лишь фиктивные вершины NIL.
Каждая вершина может быть либо красной, либо чёрной. Бесцветных вершин, или вершин другого цвета быть не может.
Каждый лист (NIL) имеет чёрный цвет.
Если вершина красная, то оба её потомка – чёрные.
Все пути от корня к листьям содержат одинаковое число чёрных вершин.
Пример КЧД с учётом наших положений приведен на рисунке 4. Учтите, что вершина 9 могла быть и красной, но в дальнейшем мы будем рассматривать только те деревья, у которых корень чёрный. Мы это сделаем для того, чтобы потомки корня могли иметь любой цвет.
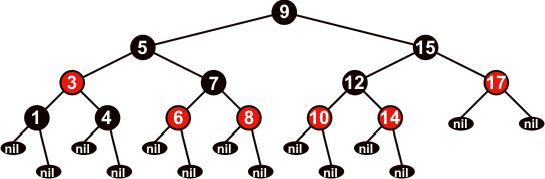
Рисунок 4.
Вращения
Операции вставки и удаления вершин в КЧД могут нарушать свойства КЧД. Чтобы восстановить эти свойства, надо будет перекрашивать некоторые вершины и менять структуру дерева. Для изменения структуры используются операции, называемые вращением. Возвращая КЧД его свойства, вращения так же восстанавливают сбалансированность дерева. Вращения бывают левые и правые, их суть показана на рисунке 5.
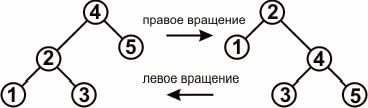
Рисунок 5.
Как видно, вращения, перемещая вершины, не нарушают свойства упорядоченности.
В процедуре RBTLeftRotate предполагается, что node.right != NIL. В процедуре RBTRightRotate предполагается, что node.left != NIL.
|
RBTLeftRotate(Tree,node) Рекомендуем скачать другие рефераты по теме: шпаргалки по математике, шпаргалки по гражданскому. Предыдущая страница реферата | 4 5 6 7 8 9 10 11 12 13 14 | Следующая страница реферата Поделитесь этой записью или добавьте в закладкиКатегории: |