Рефераты | Рефераты по информатике, программированию | Формализация понятия алгоритма |
9qSЛ |
0qoЛ |
1!Л |
||||||||
|
qs |
0qsЛ |
1qsЛ |
2qsЛ |
3qsЛ |
4qsЛ |
5qsЛ |
6qsЛ |
7qsЛ |
8qsЛ |
9qsЛ |
L!Н |
Рис.2.
Рассмотрим в качестве примера работу только что построенной Машины Тьюринга U1 для случая n=231. Первой выполненной командой будет команда 1a): 1qo®2qsH; после этой последуют команды 4b): 3qs®3qsЛ и 2b): 2qs®2qsЛ и наконец, 11b): Lqs®L!H. Таким образом, сложность этого вычислительного процесса будет равна 4.
В общем случае сложность этого алгоритма будет равна k+1, где k - число десятичных цифр в записи числа. Докажем это утверждение. Для k=1 истинность этого утверждения очевидна. Пусть это утверждение верно для k=l. Докажем, что оно сохранит истинность и для k=l+1. Появление очередной цифры в старшем разряде числа потребует от нас вместо исполнения команды Lqs® L!H или команды Lqo®1!Л либо увеличить эту цифру на 1, т.е. выполнить одну из команд в столбце а), либо “перескочить” через эту цифру, выполнив одну из команд группы b), после чего остановиться, выполнив команду 11 b). Таким образом, после обработки k цифр наша Машина Тьюринга выполнит k команд, обработка последней цифры потребует 2-х команд. Тем самым, общее количество выполненных команд будет равно l+2=(l+1)+1, что и требовалось доказать.
Обратите внимание, что вместе с оценкой сложности мы фактически доказали свойство конечности нашего алгоритма, т.е., что он обязательно остановится.
Пример 2. Построить Машину Тьюринга, вычисляющую
U((n)1)=(n-1)1 ,
где n>0 и
(n)1 означает запись числа n в унарной форме, т.е. в виде 
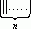. Другими словами, эта Машина Тьюринга с алфавитом D= должна
стирать одну палочку в записи числа. На рисунке 3 показана программа для этой
машины.
|
| |
L |
|||
|
qo Рекомендуем скачать другие рефераты по теме: шпоры на экзамен, реферат по математике. Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 11 | Следующая страница реферата Поделитесь этой записью или добавьте в закладкиКатегории: |
