Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10 | Следующая страница реферата

xI - входной параметр;

yI - выходной параметр.

Необходимо подобрать модель связывающую x и y.

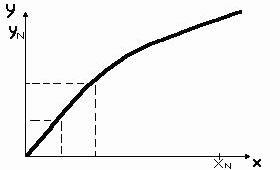
Через точки (xI,yI) можно провести кривую, которая, в свою очередь, может проходить через эти точки или находиться вблизи данных точек.

В  аппроксимации для получения параметров модели используется МНК-критерий (метод наименьших квадратов). Лучшей считается та модель, для которой сумма квадратов отклонений опытных значений, от теоретических будет минимальной.

Для этого формируется целевая функция или критерий оптимизации.

S =  ∑ (yI – F(B, xI))2 – min.

Далее надо исследовать функцию на экстремум. Неизвестными будут коэффициенты модели B. Наиболее просто находятся параметры, если F(B, xI) представляет собой полином n-ной степени. При этом формируется система линейных уравнений, порядок которой на единицу больше степени полинома. 

К примеру, для полинома 3-ей степени система будет выглядеть так:

         N       ∑ xI    ∑ xI2                 ∑ yI                      b0

С =   ∑ xI    ∑ xI2   ∑ xI3         D =  ∑ xI yI        B =    b1

         ∑ xI2   ∑ xI3   ∑ xI4                ∑ xI2 yI                  b2

C – матрица коэффициентов системы.

D – вектор-столбец свободных членов.

B – вектор неизвестных.

В общем случае для нахождения параметров формируется система дифференциальных уравнений. В конце формируется система линейных уравнений, которую можно решать точными методами (метод Крамера, Гауса, обратной матрицы). Когда система решена, то есть, найдены параметры модели, можно выполнить прогнозирование значений y.

Если выбираемое x находится внутри  элементарного интервала ∆x, то говорят о прогнозировании в настоящем. Если x меньше x0, или x больше xN, то речь идет об экстраполяции. 

 Модели интерполяции.

В интерполяции, в отличие от аппроксимации, производится минимизация линейной ошибки. Также, в отличие от аппроксимации, где кривая по отношению к точкам опытов может располагаться любым образом, а именно находиться вблизи этих точек, или проходить через некоторые из них, кривая интерполяции, или интерполяционный полином обязательно проходит через все точки кривой, которые называются узлами.

Наиболее простой подход к получению интерполяционной модели был предложен Лагранжем. Так как полином проходит через каждую опытную точку, то нужно составить столько уравнений, сколько проведено опытов. В левой части уравнения формируется полином, проходящий через i-тую точку. В правой части формируется вектор значений y. В результате получается система линейных уравнений n-ого порядка, где n – число опытов, а степень интерполяционного полинома на единицу меньше числа опытов.

Количество опытов должно обязательно быть больше пяти, иначе результаты интерполирования будут не пригодны для прогнозирования. Так как метод интерполяции требует прохождения модели через все точки, то накладываются определенные условия на опытные значения. Разности i-ого порядка должны быть примерно одинаковы малы. Хорошо интерполируются монотонные функции.

Оба рассмотренных метода относятся к методам исследования детерминированных моделей.

 Анализ временных рядов.

Временные ряды отражают тенденцию изменения параметров системы во времени, поэтому входным параметром х является момент времени.

Выходной параметр y называется уровнем ряда. В случае отсутствия ярко выраженных изменений в течение времени, общая тенденция сохраняется. Ряд можно описать уравнением вида

Рекомендуем скачать другие рефераты по теме: налоги в россии, банк курсовых работ бесплатно.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки