Предыдущая страница реферата | 5  6  7  8  9  10  11  12  13  14  15 | Следующая страница реферата

Последовательность нулей и единиц, принадлежащих данному коду, будем называть кодовым вектором.

Свойство линейных кодов: сумма (разность) кодовых векторов линейного кода дает вектор, принадлежащий данному коду.

Линейные коды образуют алгебраическую группу по отношению к операции сложения по модулю 2. В этом смысле они являются групповыми кодами.

Свойство группового кода: минимальное кодовое расстояние между кодовыми векторами группового кода равно минимальному весу ненулевых кодовых векторов.

Вес кодового вектора (кодовой комбинации) равен числу его ненулевых компонентов.

Расстояние между двумя кодовыми векторами равно весу вектора, полученного в результате сложения исходных векторов по модулю 2. Таким образом, для данного группового кода

.

Групповые коды удобно задавать матрицами, размерность которых определяется параметрами кода  и . Число строк матрицы равно , число столбцов равно +=:

                                       (71)

Коды, порождаемые этими матрицами, известны как -коды, где , а соответствующие им матрицы называют порождающими, производящими, образующими.

Порождающая матрица С может быть представлена двумя матрицами И и П (информационной и проверочной). Число столбцов матрицы П равно , число столбцов матрицы И равно :

                            (72)

Теорией и практикой установлено, что в качестве матрицы И удобно брать единичную матрицу в канонической форме:

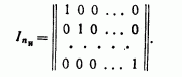
При выборе матрицы П исходят из следующих соображений: чем больше единиц в разрядах проверочной матрицы П, тем ближе соответствующий порождаемый код к оптимальному[12], с другой стороны, число единиц в матрице П определяет число сумматоров по модулю 2 в шифраторе и дешифраторе, т. е. чем больше единиц в матрице П, тем сложнее аппаратура.

Вес каждой строки матрицы П должен быть не менее , где  - вес соответствующей строки матрицы И. Если матрица И - единичная, то  (удобство выбора в качестве матрицы И единичной матрицы очевидно: при  усложнилось бы как построение кодов, так и их техническая реализация).

При соблюдении перечисленных условий любую порождающую матрицу группового кода можно привести к следующему виду:

называемому левой канонической формой порождающей матрицы.

Для кодов с =2 производящая матрица С имеет вид

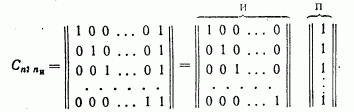
Во всех комбинациях кода, построенного при помощи такой матрицы, четное число единиц.

Для кодов с  порождающая матрица не может быть представлена в форме, общей для всех кодов с данным . Вид матрицы зависит от конкретных требований к порождаемому коду. Этими требованиями могут быть либо минимум корректирующих разрядов, либо максимальная простота аппаратуры.

Корректирующие коды с минимальным количеством избыточных разрядов называют плотно упакованными или совершенными кодами.

Рекомендуем скачать другие рефераты по теме: реферат федерация, сочинение капитанская.



Предыдущая страница реферата | 5  6  7  8  9  10  11  12  13  14  15 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки