Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Обобщив вышеизложенное можно сформулировать правило получения аналитической записи логической функции для некоторого комбинационного узла :

- для того чтобы получить аналитическое выражение функции, заданной таблично, нужно составить сумму конституент(см. ниже) единицы для тех наборов значений входных двоичных переменных, для которых реализации функции fi равны 1, причём символ любой переменной в некоторой конституенте берётся со знаком отрицания, если конкретное значение переменной xi в рассматриваемом наборе имеет значение 0 .

Поскольку логическая сумма всех элементарных произведений наивысшего ранга n обязательно равна 1, какой бы набор значений входных переменных ни рассматривался, то эти произведения вполне логично называть конституентами (составляющими) единицы. Аналогично объясняется и название конституенты (составляющей) нуля, так как известно, что логическое произведение всех элементарных сумм наивысшего ранга тождественно равно нулю .

Все функции, полученные в соответствии с вышеизложенным правилом получения аналитической записи логической функции для некоторого комбинационного узла, независимо от числа аргументов имеют много общего в своей структуре. Таким образом это правило определяет канонический вид любой логической функции. В этом случае говорят, что функция задана (записана) в совершенной дизъюнктивной нормальной форме (СДНФ). Нормальной эта форма называется потому, что члены функции в данном случае имеют вид элементарных конъюнкций. Вследствие того что все члены соединены в одну функцию знаком дизъюнкции, форма носит название дизъюнктивной. И, наконец, форма называется совершенной, так как все её члены имеют высший ранг, являясь конституентами единицы .

Поскольку алгебра логики симметрична, то вышеприведённые рассуждения можно применить для вывода ещё одной канонической формы логических функций - совокупности конституент нуля, соединённых знаком конъюнкции.  Таким образом сформулируем второе правило :

- для того чтобы получить аналитическое выражение функции, заданной таблично, в совершенной конъюктивной нормальной форме, нужно составить логическое произведение конституент нуля для тех наборов значений, входных двоичных переменных, для которых реализация функции fi равна 0, причём символ любой переменной в некоторой конституенте берётся со знаком отрицания, если её конкретное значение xi в рассматриваемом наборе равно 1 .

В общем случае переход к совершенной нормальной форме производится за три шага .

1-й шаг - с помощью многократного применения законов инверсии снимаются общие и групповые отрицания так, чтобы отрицания оставались только у одиночных переменных .

2-й шаг - с помощью распределительных законов производится переход к одной из нормальных форм функции.

3-й шаг - производится преобразование членов ДНФ или КНФ в соответствующие конституенты с помощью правила развёртывания .

Пользуясь сформулированными правилами и таблицей 1.1 для полусумматора записываем :

                           p(x1,x2) = x1x2

                           s(x1,x2)= x1x2 +x1x2                                              СДНФ     (1.3)

                           p(x1,x2) = (x1+ x2) (x1 +x2) (x1+x2)

                           s(x1,x2) = (x1+ x2) (x1 +x2)                               СКНФ     (1.4)

3-й этап синтеза - анализ и оптимизация (минимизация) логических функций являются весьма важными компонентами синтеза цифровых автоматов без памяти.  Поэтому методы анализа и оптимизации будут рассмотрены отдельно .

4-й этап синтеза - к построению функциональной схемы синтезируемого узла в принципе можно переходить сразу же, как только становится известным аналитическое описание его работы.  Построение схемы основано на прямом замещении элементарных произведений, сумм и отрицаний соответственно конъюнкторами, дизъюнкторами и инверторами. Пользуясь соотношениями (1.3), (1.4) можем построить для полусумматора две функциональные схемы .

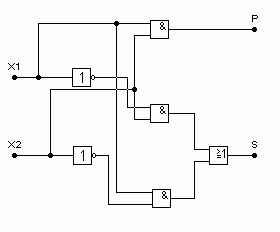                       а) СДНФ

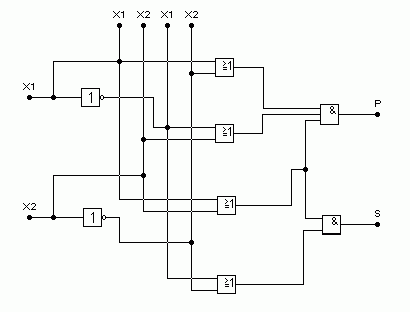б) СКНФ

     Рис. 1.1 Функциональная схема полусумматора .

С функциональной точки зрения обе схемы полностью тождественны, хотя по структурной сложности они значительно различаются .

 1.2. Общие сведения о минимизации логических функций

Однозначность соответствия формы логической функции и параметров реальной электронной схемы приводит к необходимости оптимизации функции, т.е. к необходимости получения наилучшего её вида по выбранному критерию. В общем случае речь должна идти об оптимизации функции по таким показателям, как быстродействие, надежность (достижение их максимума), количество потребного оборудования, вес, габариты, энергопотребление, стоимость (достижение их минимума) и т.п. Однако решение этой задачи в общем виде- достаточно трудное дело, тем более что некоторые из указанных показателей находятся в известном противоречии. Например, увеличение быстродействия, как правило, достигается за счет параллельной организации работы данного устройства, но это ведёт к увеличению оборудования, а значит, к уменьшению надежности и увеличению стоимости. Поэтому на практике обычно решается частная задача оптимизации по одному из критериев. Чаще всего это делается по минимуму потребного оборудования, так как при этом автоматически решаются задачи получения минимальных габаритов, веса, энергопотребления, стоимости. Такая частная задача оптимизации логической функции носит название минимизации.

Таким образом, возникает задача нахождения из всех возможных форм логической функции её так называемой минимальной формы, обеспечивающей минимум затрат оборудования при построении синтезируемого узла, если имеется заданный набор логических элементов (НЕ, И, ИЛИ) с определенными техническими характеристиками (например, максимально возможное число входов у элементов И,  ИЛИ и др.). Нетрудно заметить, что в рамках нормальных форм минимальной будет такая разновидность функции, которая состоит из наименьшего количества членов при наименьшем, по возможности, общем числе символов переменных.

Из большего числа различных приемов и методов минимизации рассмотрим три наиболее показательных, типовых:

Рекомендуем скачать другие рефераты по теме: лес реферат, анализ дипломной работы.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки