Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата

P - давление, под которым жидкость подается в щель формообразователя;

R и R1 - главные радиусы кривизны столбика расплава;

y - высота подъема мениска.

Знак “+” относится к вогнутому столбу, а “—” к выпуклому. Дифференциальное уравнение профильной кривой приближенно, но достаточно точно описывается выражением:

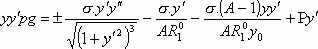          (8)

где       ,---первая и вторая производная по х;

На рис. 3 приведены параметры столба расплава, для которого написано уравнение (8). Начало координат располагается на уровне основания столба расплава. С. В. Цивинский, П. И. Антонов, А. В. Степанов вывели аналитическое уравнение столба расплава при выращивании кристаллов любой заданной формы. Замена cos a производными и интегрирование уравнения (8) от y0 до y дает выражения:

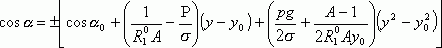;              (9)

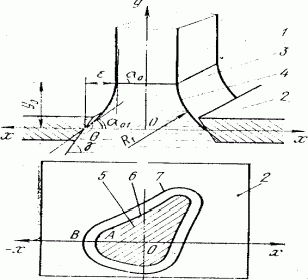
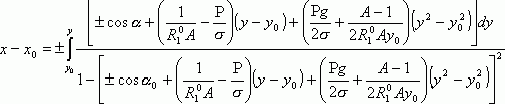.          (10)

(Рис.3)

Схема формирования мениска расплава при вытягивании кристалла с поперечным сечением произвольной формы. Параметры столба расплава:

высота столба расплава y0:

угол наклона касательной к профильной крывой к оси х (угол a01, при y=0 и угол a0 при y = y0); радиус кривизны поверхности столба расплава, лежащего в плоскости, перпендикулярной касательной ( при  при );

1 — кристалл; 5 — формообразователь; 3—столб расплава;

4—профильная кривая столба расплава: S—поперечное сечение вытягиваемого кристалла;

6—контур поперечного сечения кристалла; 7—контур отверстия в формообразователе.

Уравнение (10) представляет собой уравнение профильной кривой вогнутого и выпуклого столбов расплава в общем виде. Интеграл в уравнении (10) не выражается в элементарных функциях и может быть вычислен только численно. Знак “—” перед интегралом соответствует левой (по отношению к оси) ветви, а “+”—правой ветви меридиональной кривой. Обе ветви равноправны.

Ограничиваясь для простоты описанием только левой ветви и принимая, например, для выпуклого столба допущение cos a p/2). Формообразователь постепенно погружается в расплав (рис. 12,а), проходя ряд последовательных положений — от I до V. В положении формообразователь касается расплава нижней плоскостью. Давление, при котором расплав подается в щель (Р), равно нулю, а угол между стенкой щели и поверхностью расплава g=p/2.

При дальнейшем погружении формообразователя угол у увеличивается вплоть до величины q. В момент, когда глубина погружения равна (t0+t), линия контакта расплава в формообразователе совпадает с его верхней кромкой (положение IV), и при последующем повышении давления должно иметь место условие “зацепления”. При этом угол g растет до значения 0+л/2, т.е. достигает угла смачивания с горизонтальной поверхностью формообразователя. Дальнейшее погружение формообразователя приводит к растеканию капли.

Как следует из приведенного рисунка, положения II—V соответствуют выпуклым столбам расплава, которые могут быть образованы внутри формообразующего отверстия (положения I - III) или над ним (IV—V). Таким образом, образование столба расплава происходит в формообразователе под действием давления расплава без затравки.

Произведем касание затравки с мениском типа IV или V в предположении, что площадь сечения затравки много меньше площади формообразующего отверстия. При этом образуется граница фазовый переход—фронт кристаллизации и устанавливается его начальное положение (VI).

И, наконец, собственно выращивание кристалла включает в себя ряд переходных состояний фронта кристаллизации—от начального положения V! до положения VIII.

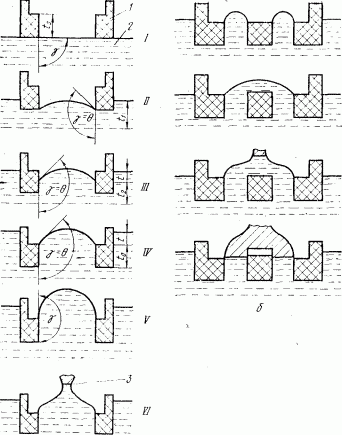
РИС. 12.

Рекомендуем скачать другие рефераты по теме: оформление доклада, курсовая работа по управлению.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки