Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

P - давление, под которым жидкость подается в щель формообразователя;

R и R1 - главные радиусы кривизны столбика расплава;

y - высота подъема мениска.

Знак “+” относится к вогнутому столбу, а “—” к выпуклому. Дифференциальное уравнение профильной кривой приближенно, но достаточно точно описывается выражением:

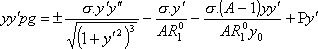          (8)

где       ,---первая и вторая производная по х;

На рис. 3 приведены параметры столба расплава, для которого написано уравнение (8). Начало координат располагается на уровне основания столба расплава. С. В. Цивинский, П. И. Антонов, А. В. Степанов вывели аналитическое уравнение столба расплава при выращивании кристаллов любой заданной формы. Замена cos a производными и интегрирование уравнения (8) от y0 до y дает выражения:

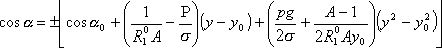;              (9)

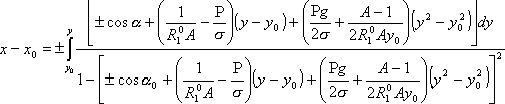.          (10)

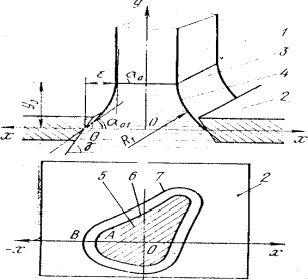
(Рис.3)

Схема формирования мениска расплава при вытягивании кристалла с поперечным сечением произвольной формы. Параметры столба расплава:

высота столба расплава y0:

угол наклона касательной к профильной крывой к оси х (угол a01, при y=0 и угол a0 при y = y0); радиус кривизны поверхности столба расплава, лежащего в плоскости, перпендикулярной касательной ( при  при );

1 — кристалл; 5 — формообразователь; 3—столб расплава;

4—профильная кривая столба расплава: S—поперечное сечение вытягиваемого кристалла;

6—контур поперечного сечения кристалла; 7—контур отверстия в формообразователе.

Уравнение (10) представляет собой уравнение профильной кривой вогнутого и выпуклого столбов расплава в общем виде. Интеграл в уравнении (10) не выражается в элементарных функциях и может быть вычислен только численно. Знак “—” перед интегралом соответствует левой (по отношению к оси) ветви, а “+”—правой ветви меридиональной кривой. Обе ветви равноправны.

Ограничиваясь для простоты описанием только левой ветви и принимая, например, для выпуклого столба допущение cos a<<1, получаем:

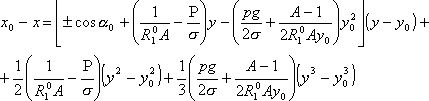                   (11)

Для построения профильной кривой по уравнению (11) необходимо знать углы наклона профильной кривой мениска расплава к горизонтали у поверхности кристалла a0 и у кромки формообразователя a01. Угол a0 рассчитать трудно: он зависит от положения фронта кристаллизации по оси н, от формы фронта кристаллизации и др. Наблюдения формы мениска расплава при выращивании кристаллов германия способом Чохральского, сделанные П. И. Антоновым  и М. Шашковым , дали значения a0=70—80°. В случае, близком к отрыву кристалла от расплава, a0 @ p / 2. Как следует из рис. 3, угол a01 может быть вычислен по соотношениям:

для вогнутого столба расплава

для выпуклого столба расплава                                                              (12)

Рекомендуем скачать другие рефераты по теме: налоги в россии, банк курсовых работ бесплатно.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки