
Становление радиотехнической теории: от теории к практике. На примере технических следствий из открытия Г. Герца
Категория реферата: Рефераты по истории техники
Теги реферата: сочинение ревизор, мтс сообщения
Добавил(а) на сайт: Nikolenko.
1 2 3 4 5 6 7 8 | Следующая страница реферата
Становление радиотехнической теории: от теории к практике. На примере технических следствий из открытия Г. Герца
Горохов Виталий Георгиевич - доктор философских наук, Институт философии РАН
Фундаментальные и прикладные исследования в технических науках: понятие технической теории
Классические технические науки, как хорошо известно, тесно связаны с естественными науками. Они испытывают их влияние и в процессе своего функционирования, получая от них исходные теоретические представления, а именно: идеальные объекты и понятия, способы математических описаний, а также сами идеалы научности. В то же время в технических науках все эти взаимосвязанные в новую техническую теорию элементы существенно трансформируются и в результате формируется новый тип организации теоретических знаний. Можно с полным правом сказать, что и технические науки, в свою очередь, стимулируют развитие естествознания, ставя перед ними новые проблемы и темы для исследования.
Особенность научно-технических дисциплин состоит в том, что в них инженерная деятельность часто не только дополняет эксперимент, но и заменяет его, выполняя его функцию. Именно в ней проверяется адекватность теоретических выводов и выявляется новый эмпирический материал для исследования. Поэтому научно-технические дисциплины должны доводить теоретические знания до уровня практических инженерных рекомендаций. Специфика технической теории выражается не столько в использовании ее выводов для объяснения природных процессов, протекающих в технических устройствах, или даже не только в необходимости доказательства применимости ее результатов на практике, сколько в их регулярном практическом использовании для создания этих технических устройств.
Российский ученый С.А. Христианович, исследуя движение грунтовых вод через крупнозернистые пески или щебень, показал, что в данном случае закономерность, установленная в рамках естественно-научной дисциплины, для соотношения между уклоном и скоростью фильтрации однородной несжимаемой жидкости, становится неверной, так как в ней не учитывается целый ряд важных для решения практических инженерных задач факторов. Чтобы вывести более адекватные уравнения движения грунтовых вод, Христианович строит новый идеальный объект, используя полученные в инженерной практике данные: "Пусть фильтрация происходит через грунт, заключенный в трубке настолько тонкой, что в плоскости ее поперечного сечения напор можно считать постоянным". Причем рассматривается идеализированный "случай однородного грунта, изотропного в отношении фильтрационных свойств". Для решения сформулированной таким образом теоретически проблемы привлекаются данные технически подготовленного идеализированного эксперимента. "Закон фильтрации для такого грунта, т.е. зависимость между падением напора и расходом или скоростью фильтрации, может быть установлен, например, из опытов над фильтрацией через образцы, заключенные в трубках" [1]. Далее Христианович от теоретически созданного идеального объекта переходит к исследованию грунтовых вод в земляном массиве, т.е. к реальным условиям.
В технических науках проводятся специальные теоретические (иначе говоря, специфические фундаментальные) исследования. Анализ этих исследований становится одной из важных задач современной методологии науки. Поэтому важно провести различение теоретического и эмпирического уровней технического знания. Эмпирические технические знания включают в себя практико-методические, технологические и конструктивно-технические знания. Первые связаны с деятельностью субъекта по созданию определенного продукта, вторые - это знания о взаимодействии преобразуемого объекта и используемых для этого орудий труда, т.е. в широком смысле о методах создания артефактов и принципах их применения. Конструктивно-технические знания отражают структурные и функциональные особенности различных конструктивных элементов технического устройства.
В структуре технической теории можно выделить три типа теоретических схем: функциональные схемы, имеющие целью математическое описание; "процессуальные" схемы, выделяющие в техническом устройстве протекающие в нем естественные (в особенности физические) процессы, т.е. процессы функционирования; структурные схемы, представляющие параметры и расчеты конструкции, т.е. структуры этого устройства.
В процессе становления технической теории функциональные схемы возникают на основе исходных математических моделей, а процессуальные схемы строятся на базе представлений соответствующей базовой естественнонаучной теории.
Формирование технической теории происходит, как правило, следующим образом. В начале возникает задача создания технического устройства определенного типа. Прежде всего эта задача формулируется в виде определенной структурной схемы, которая затем редуцируется до представления о физическом процессе, протекающем в данном устройстве.
Инженерная задача переформулируется в виде научной проблемы, а затем математической задачи, решаемой дедуктивным путем. Этот путь "снизу вверх" называется анализом схем, а противоположный ему - синтезом схем, он позволяет на базе уже имеющихся конструктивных элементов, точнее соответствующих им идеальных объектов, синтезировать новое техническое устройство (вернее, его идеальную модель или теоретическую схему) по определенным правилам дедуктивного преобразования, рассчитать его основные параметры и проимитировать его функционирование. Выработанное на идеальной модели решение затем последовательно переносится на уровень инженерной практики. Главная задача технической теории состоит в разработке разных типов структурных схем для различных (всевозможных) требований и условий. Тем самым заранее теоретически обеспечивается создание соответствующих технических устройств.
Математические модели выполняют в технической теории разные функции, без них, в частности, невозможны инженерные расчеты. Кроме того, в развитой технической теории эти модели используются для анализа и синтеза теоретических схем. Применение математических методов для конструирования идеальных объектов служит развитию технической теории. Исследование математических моделей позволяет получать новые знания о процессах, протекающих в технических устройствах, без обращения к инженерной практике или эксперименту, а математические методы в процессе их применения и сами претерпевают определенные изменения. Они приспосабливаются к решению специфических научно-технических задач. Именно таким образом, например, возникло операционное исчисление, развитое первоначально для решения практических инженерных задач и получившее свою совершенную логическую форму значительно позже.
Операционное исчисление было создано английским инженером Оливером Хевисайдом (1850-1925). Он значительно упростил уравнения Максвелла, записав их в векторной форме вместо использовавшейся ранее кватернионной. На практике это означало, что вместо 20 уравнений с 20 переменными, надо было решать четыре уравнения для двух переменных - векторов электрического и магнитного поля. Благодаря этому векторы вошли в обиход у физиков. Впоследствии он сумел решить задачу передачи электромагнитного сигнала по проводам [2]. "Между 1880 и 1887 гг. Хевисайд разработал операционное исчисление [...] метод решения дифференциальных уравнений с помощью преобразования их в обычные алгебраические [...] Ему принадлежит знаменитая фраза: "Математика - экспериментальная наука, а определения появляются не вначале, а значительно позже". Этой фразой он ответил на критику использования операторов до того, как они ясно определены" [3]. "О. Хевисайд при исследовании в конце XIX в. переходных явлений в телефонных линиях связи разработал и применил операционное исчисление, явившееся эффективным аппаратом математического исследования многих прикладных вопросов [...] Однако этот метод не был им строго обоснован с математической точки зрения [...] Простота и эффективность этого метода при исследовании переходных явлений в электрических цепях были разительным очевидным фактом. Метод Хевисайда в 1920-х гг. стал предметом специальных математических исследований, и его строгое обоснование в трудах Д. Карсона, Т. Бромвича, К. Вагнера, П. Леви положило начало операционному исчислению как области математики" [4]. Хевисайд внес "большой вклад в дальнейшее развитие теории электрических цепей. При этом он придавал огромное значение именно эффективным методам расчета. В особенности он увлекся "алгебраическими формулировками". Но уровень развития алгебраических методов в то время был еще не достаточен, и их успех не мог быть полным. Операционное исчисление принесло Хевисайду бессмертную славу, но это потом, а для начала он попал под огонь бешеной критики. Он не дожил до воплощения в жизнь своих идей. Прежде всего Вагнер, Кэмпбелл и Бромвич обосновали в 1916 году с помощью вспомогательных алгебраических средств метод Хэвисайда. Позже Ван дер Пол (начиная с 1929 г.), Кэмпбелл, Вагнер, Дойч (начиная с 1937 г.) и др. пытались обосновать его метод с помощью теории функций [...] Но выбранный ими путь вел в прямо противоположном направлении, чем то, на которое указывал Хевисайд. Лишь Й. Микусинский (в 1950 г.) впервые показал в своих работах [...], как можно реализовать алгебраические идеи Хевисайда. Затем Йошида (1980) доработал важнейшую для теории систем и теории электрических цепей часть его идей. Предварительный итог развитию этого направления дают работы, выполненные автором данной книги в сотрудничестве с математиком В. Мартеном на основе некоторых работ Г. Вунша [...] При этом стало возможным показать, что восходящий еще к Ч. Штейнмецу [...] символический метод может быть заменен алгебраическим исчислением [...], которое по своей алгебраической структуре аналогично доработанному исчислению Хевисайда-Йошида" [5].
Применение математики хотя бы для проведения инженерных расчетов уже требует определенной идеализации технических систем. Исследователь - представитель технической науки - работает одновременно с теоретическими схемами, как физической, так и технической теории, а также с математическими моделями, которые интерпретируются, с одной стороны, с точки зрения их физического смысла, а с другой - с позиций содержания инженерной деятельности. Его собственная деятельность заключается в поиске научного обоснования средств идеального описания стоящих перед ним познавательных задач, которые, однако, выявляются в процессе инженерной деятельности. Данная идеализация строится так, чтобы теоретические схемы оказались согласованы друг с другом, будто слои единого целого, и так, чтобы было возможно, переходя от слоя к слою, прийти к математической модели, которую проектировщик мог бы использовать в расчетах новой техники.
Последовательную универсальную для исследования различного рода механизмов теоретическую схему разработал в конце прошлого столетия российский машиновед В. Л. Ассур (1878-1920) исходя из единых принципов их структурной классификации. Такая схема давала возможность не только распределять механизмы на группы по общим признакам, но и применять общие методы решения задач. Некоторые из них были разработаны самим Ассуром, например, методы "особых точек", "ложных картин скоростей" и т.п., иные же, разработанные другими учеными и инженерами ранее, он включил в контекст своей классификации. Эти методы заключались в установлении соответствия между геометрическими представлениями механизма (функциональными схемами) и его кинематическими (поточными) схемами. Тогда с помощью некоторых дополнительных графических построений (построения годографов скоростей и ускорений), а также решения некоторых систем уравнений удается определить опасные значения напряжений и методами теории механизмов и машин изменить в нужном направлении создавшееся положение. Иными словами, инженерная задача разработки надежного, прочного и длительно действующего механизма сводится к научной проблеме исследования, что в контексте физического представления означает определить силы, действующие на его звенья. При этом сам механизм рассматривается как некоторое физическое тело, в естественном, а не искусственном модусе рассмотрения. Далее модифицируя эту научную проблему в математическую задачу, необходимо представить механизм и его движения уже не как движения физического тела, а как ряд геометрических фигур, каждая из которых соответствует определенному положению элементов механизма, причем его элементы рассматриваются теперь в виде математических точек, а силы, на них действующие, - в виде векторов [6]. Таким образом, в работах Добровольского и Артоболевского впервые было осуществлено проецирование теоретической модели на класс потенциально возможных (гипотетических) технических систем определенного типа - механизмов. Сам Артоболевский следующим образом характеризует полученные результаты: "1. Законы структурного образования являются общими для всех механизмов. 2. Анализ общих законов структуры механизмов позволяет установить все возможные семейства и роды механизмов, а также создать единую общую классификацию механизмов. 3. Структурный и кинематический анализ механизмов одного и того же семейства и класса может быть проведен аналогичными методами [...] 4. Проведенные исследования показывают, что современная техника использует очень малое количество механизмов. Предлагаемый [...] метод структурного анализа дает возможность обнаружить огромное число новых механизмов, до сих пор не применявшихся в технике. Эти новые виды механизмов могут быть рекомендованы к использованию на практике" [7].
Таким образом, современные научно-технические дисциплины нельзя рассматривать лишь как прикладные области соответствующих естественных наук, так как в них построены собственные технические теории.
Исследуем далее, каким образом из электродинамики в результате модификации ее исходной теоретической схемы, развитой в первую очередь в работах Генриха Герца, формируется подобная ей, но отличающаяся от нее структура радиотехнической теории [8]. К моменту появления теоретических основ радиотехники еще не было соответствующей ей развитой отрасли промышленности, которая формировалась параллельно с разработкой теоретических схем радиотехники. Поэтому в этом случае теоретическая радиотехника может служить своего рода идеализированным объектом - идеальным типом - историко-научного и методологического анализа генезиса теоретических схем технических наук в процессе модификации теоретических схем соответствующей базовой физической теории (электродинамики).
Экспериментальное доказательство Герцем теории Максвелла и его технические следствия
Заимствованная из механики и акустики теоретическая схема естественного волнового процесса позволяла транслировать для случая электромагнитных волн и соответствующую математическую схему - геометрическое изображение стоячей волны с ее узлами, пучностями, периодом, фазой и длиной. Пользуясь этой схемой Генрих Герц поставил соответствующие эксперименты и произвел необходимые измерения: в частности, изменения фазы и амплитуды электромагнитных волн при отражении и показателя преломления асфальтовой призмы. Герц также, как и Максвелл, использовал Фарадеево представление об электрических и магнитных силовых линиях, детализировав его. Например, он приводит изображения так называемого процесса "отшнуровывания" силовых линий от вибратора (колебательного контура), ставшего затем очень важным для радиотехники элементом радиопередающего устройства, анализируя распределение сил для различных моментов времени. Он называет такое изображение "наглядной картиной распределения силовых линий" (см. рис. 1) [9].
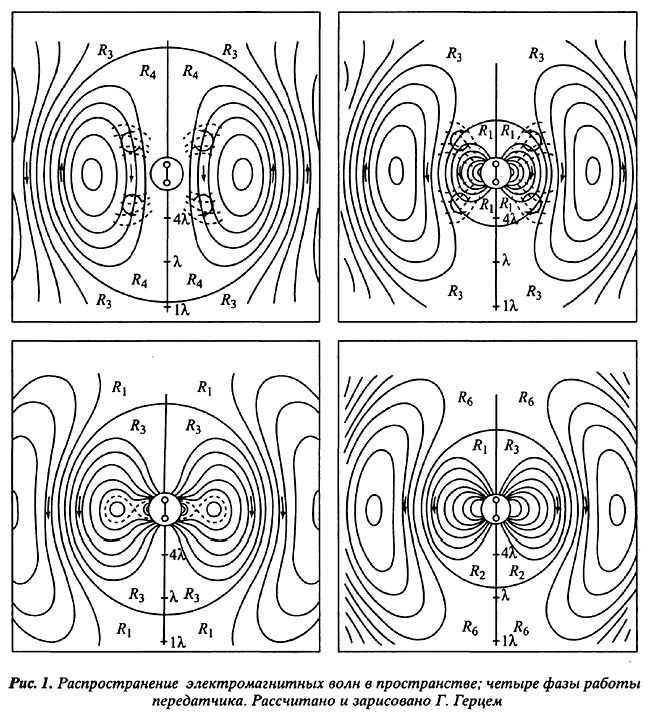
Герц строит особые структурные теоретические схемы и соответствующий им концептуальный аппарат (например, понятия вибратора и резонатора). Скрупулезное описание конструкции опытного оборудования (в том числе, материала, из которого изготовлены зеркала, их формы и размеров) сочетается у него с обобщенным теоретическим описанием экспериментально-измерительных ситуаций в виде структурных схем, которые являются прообразом будущих электрических схем радиоприемного и радиопередающего устройств и входят в состав физической теории (вибратор и резонатор). Для регистрации искры он искал сначала позицию микрометра, соединенного проводом с вибратором, а затем отсоединенного от него, что позволило ему открыть беспроводную передачу электромагнитных волн (см. рис. 2-А) [10].
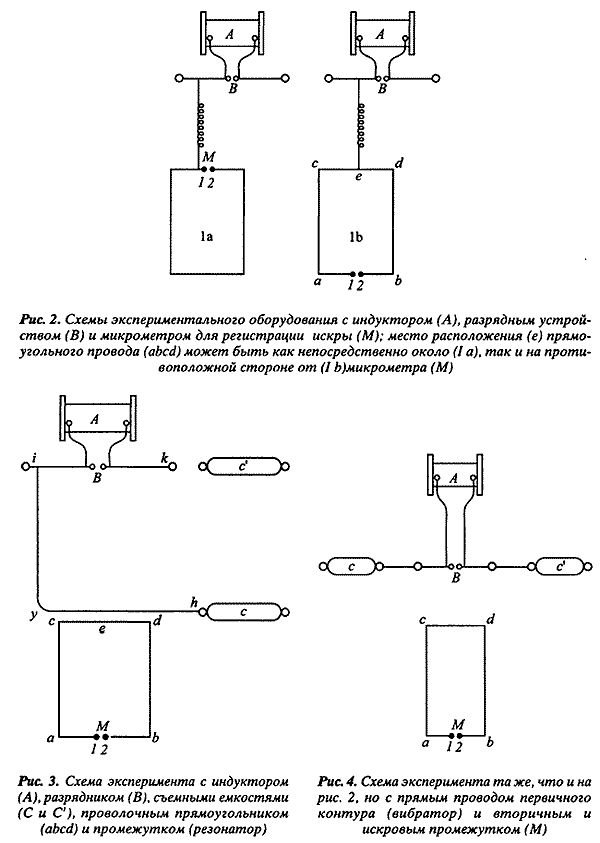
При исследовании явления электромагнитного резонанса Герцу приходилось подбирать нужные параметры различных компонентов его установки, включавших индукционную катушку, разрядник, конденсатор и т.д. Он измерял длину искры и расстояние между вибратором и резонатором, на основе этих измерений вычерчивал резонансные кривые и проводил необходимые расчеты. Разрабатывая новое экспериментальное оборудование, он действовал как инженер, хотя и не имел в виду какого-либо технического применения своих экспериментальных устройств. И математический аппарат, и опыты служили ему лишь средством к пониманию и объяснению физического процесса - распространения электромагнитных волн в пространстве. Но благодаря именно его работам электродинамика смогла дать жизнь новой сфере инженерной деятельности и соответствующей ей технической теории.
Свою хорошо оснащенную лабораторию в университете Карлсруэ Герц унаследовал от Фердинанда Брауна, профессора электротехники, модернизировавшего в 1883-1885 гг. курсы соответствующих дисциплин в этом университете. Уже "в его ранних исследованиях, которые он проводил задолго до возникновения беспроволочной телеграфии, можно обнаружить зародыши важнейших разработок в этой области [...] Он обладал огромным даром и необыкновенным искусством создания вспомогательного экспериментального оборудования. Именно таким образом появилась измерительная аппаратура, имеющая большое самостоятельное значение, которая нашла применение в качестве физической исследовательской и измерительной техники", - писали о Брауне Мандельштам и Папалекси в 1928 г. [11]
Когда Герц прибыл в Карлсруэ, перед ним "была поставлена задача читать лекции по физическому эксперименту для студентов инженерных специальностей. Для решения этой задачи у него в распоряжении было все необходимое физическое оборудование, которое он мог также использовать и для исследовательских целей" [12]. Позже Герц писал:
Рекомендуем скачать другие рефераты по теме: заболевания реферат, конспект урока по математике.
1 2 3 4 5 6 7 8 | Следующая страница реферата