
Анализ и решение проблемы переноса энергии волнами электромагнитного поля
Категория реферата: Рефераты по математике
Теги реферата: франция реферат, изложение дубровский
Добавил(а) на сайт: Savvatej.
Предыдущая страница реферата | 1 2 3 4 | Следующая страница реферата
Усредняя
это выражение по времени (по периоду колебаний), имеем ![]() , то есть мы
приходим здесь к физически разумному результату, когда посредством обсуждаемой
гипотетической волны в пространстве без потерь переносится ЭМ энергия
, то есть мы
приходим здесь к физически разумному результату, когда посредством обсуждаемой
гипотетической волны в пространстве без потерь переносится ЭМ энергия ![]() , не зависящая
от времени и точек пространства. Следовательно, при таком волновом процессе, как и должно быть, имеем закон сохранения энергии. К сожалению, как мы
убедились выше, это невозможно в принципе, поскольку, согласно уравнениям
Максвелла (1), ЭМ волн с такими характеристиками в Природе нет.
, не зависящая
от времени и точек пространства. Следовательно, при таком волновом процессе, как и должно быть, имеем закон сохранения энергии. К сожалению, как мы
убедились выше, это невозможно в принципе, поскольку, согласно уравнениям
Максвелла (1), ЭМ волн с такими характеристиками в Природе нет.
Итак, проблема с выяснением физического механизма переноса энергии волнами ЭМ поля
объективно существует, и для ее разрешения требуется, по всей видимости, весьма
нестандартный эвристический подход. Однако в наличии у нас имеется только
система уравнений электродинамики Максвелла, а потому для разрешения
обсуждаемого здесь парадокса ничего не остается, как продолжить критический
анализ именно уравнений (1) с целью поиска новых (скрытых) реалий в их
физическом содержании. И, действительно, такие реалии в уравнениях (1) были
обнаружены [3], а их суть заключена в соотношениях первичной взаимосвязи ЭМ
поля с компонентами электрической ![]() и магнитной
и магнитной ![]() напряженности и поля ЭМ векторного потенциала
с электрической
напряженности и поля ЭМ векторного потенциала
с электрической ![]() и магнитной
и магнитной ![]() компонентами:
компонентами:
(a)
![]() , (b)
, (b) ![]() , (5)
, (5)
(c)
![]() , (d)
, (d) ![]() .
.
Соотношение
(5a) вводится с помощью уравнения (1d), поскольку дивергенция ротора
произвольного векторного поля тождественно равна нулю. Соответственно, (5b)
следует из уравнения (1b) при ![]() , справедливого для сред с локальной электронейтральностью. Далее подстановка
(5a) в (1а) дает (5c), а подстановка (5b) в (1c) приводит к (5d). Здесь два
(даже три) представленных соотношения достаточно известны [1], а соотношение
(5d), по-видимому, просто не сочли достойным должного внимания.
, справедливого для сред с локальной электронейтральностью. Далее подстановка
(5a) в (1а) дает (5c), а подстановка (5b) в (1c) приводит к (5d). Здесь два
(даже три) представленных соотношения достаточно известны [1], а соотношение
(5d), по-видимому, просто не сочли достойным должного внимания.
Однако
объединение полученных соотношений в систему (5) оказалось весьма
конструктивным, поскольку в этом случае возникает система дифференциальных
уравнений, описывающих значительно более сложное и необычное с точки зрения
общепринятых воззрений вихревое векторное поле в виде совокупности
функционально связанных между собой четырех вихрево-полевых компонент ![]() ,
, ![]() и
и ![]() ,
, ![]() , которое
физически логично назвать реальным электромагнитным полем.
, которое
физически логично назвать реальным электромагнитным полем.
Объективность
существования указанного четырехкомпонентного вихревого поля иллюстрируется
нетривиальными следствиями из полученных выше соотношений, поскольку
подстановки (5c) в (5b) и (5d) в (5a) приводят к системе новых
электродинамических уравнений, структурно полностью аналогичной системе
традиционных уравнений Максвелла (1), но уже для поля ЭМ векторного потенциала
с электрической ![]() и магнитной
и магнитной ![]() компонентами:
компонентами:
(a)
![]() , (b)
, (b) ![]() , (6)
, (6)
(c)
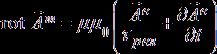 , (d)
, (d) ![]() .
.
Чисто вихревой характер компонент поля векторного потенциала обеспечивается условием кулоновской калибровки посредством дивергентных уравнений (6b) и (6d), которые при этом представляют собой начальные условия в математической задаче Коши для уравнений (6a) и (6c), что делает эту систему уравнений замкнутой.
Соответственно, математические операции с соотношениями (5) позволяют получить [3] еще две других системы уравнений:
для
электрического поля с компонентами ![]() и
и ![]()
(a)
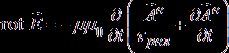 , (b)
, (b) ![]() , (7)
, (7)
(c)
![]() , (d)
, (d) ![]() ,
,
и
для магнитного поля с компонентами ![]() и
и ![]() :
:
(a)
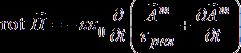 , (b)
, (b) ![]() , (8)
, (8)
(c)
![]() , (d)
, (d) ![]() .
.
Кстати, если считать соотношения (5) исходными, то из них подобным образом следуют и
уравнения системы (1), справедливые для локально электронейтральных сред (![]() ). Таким
образом, система уравнения (5) первичной взаимосвязи компонент ЭМ поля и поля
ЭМ векторного потенциала, безусловно, фундаментальна.
). Таким
образом, система уравнения (5) первичной взаимосвязи компонент ЭМ поля и поля
ЭМ векторного потенциала, безусловно, фундаментальна.
Далее, как и должно быть, из этих систем электродинамических уравнений непосредственно следуют (аналогично выводу формулы (2)) соотношения баланса:
судя по размерности, для потока момента ЭМ импульса из уравнений (6)
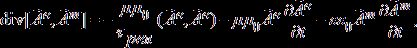 (9)
(9)
для потока электрической энергии из уравнений (7)
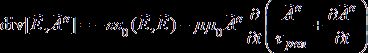 (10)
(10)
и, наконец, для потока магнитной энергии из уравнений (8)
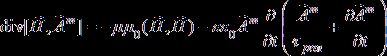 . (11)
. (11)
Рекомендуем скачать другие рефераты по теме: скачать на телефон шпаргалки, сочинение.
Предыдущая страница реферата | 1 2 3 4 | Следующая страница реферата