Аппроксимация функций

Из курса математики известны 3 способа задания функциональных зависимостей:

аналитический графический табличный

Табличный способ обычно возникает в результате эксперемента.

Недостаток табличного задания функции заключается в том, что найдутся значения переменных которые неопределены таблицей. Для отыскания таких значений определяют приближающуюся к заданной функцию, называемой аппроксмирующей, а действие замены аппроксимацией.

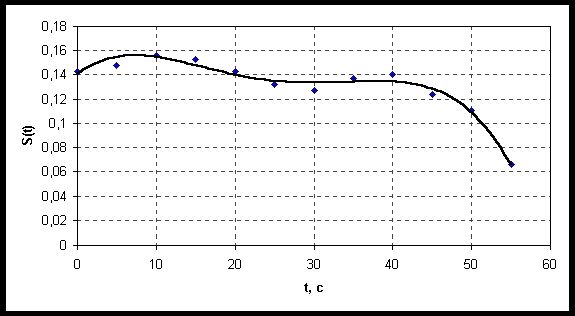
Аппроксимация заключается в том, что используя имеющуюся информацию по f(x) можно рассмотреть другую функцию φ(ч) близкую в некотором смысле к f(x), позволяющую выполнить над ней соответствующие операции и получить оценку погрешность такой замены.

φ(υ)- аппроксимирующая функция.

Интерполяция (частный случай аппроксимации)

Если для табличной функции y=f(x), имеющей значение x0 f(x0) требуется построить аппроксимирующюю функцию j (x) совпадающую в узлах с xi c заданной, то такой способ называется интерполяцией

При интерполяции, заданная функция f(x) очень часто аппроксимируется с помощью многочлена, имеющего общий вид

j (x)=pn(x)=anxn+an-1xn-1+…+a0

В данном многочлене необходимо найти коэффициенты an ,an-1, …a0 , так как задачей является интерполирование, то определение коэффициентов необходимо выполнить из условия равенства:

Pn(xi)=yi i=0,1,…n

Для определения коэффициентов применяют интерполяционные многочлены специального вида, к ним относится и полином Лагранжа Ln(x).

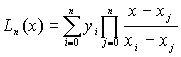i¹ j

В точках отличных от узлов интерполяции полином Лагранжа в общем случае не совпадает с заданной функцией .

Задание

С помощью интерполяционного полинома Лагранжа вычислить значение функции y в точке xc, узлы интерполяции расположены равномерно с шагом D х=4,1 начиная с точки х0=1,3 даны значения функции y={-6.56,-3.77,-1.84,0.1,2.29,4.31,5.86,8.82,11.33,11.27}.

ГСА для данного метода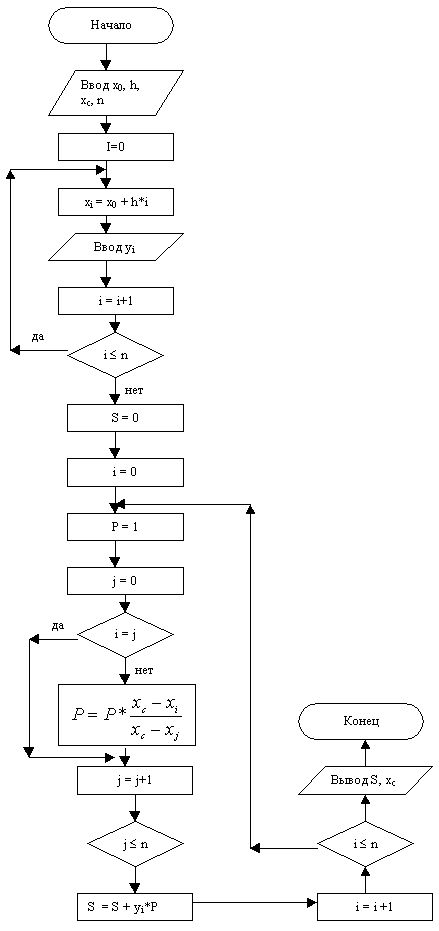

CLS

DIM Y(9)

DATA -6.56,-3.77,-1.84,0.1,2.29,4.31,5.86,8.82,11.33,11.27

X0 = 1.3: H = 4.1: N = 10: XC = 10

FOR I = 0 TO N - 1

1 X(I) = X0 + H * I

READ Y(I)

PRINT Y(I); X(I)

NEXT I

S1 = 0: S2 = 0: S3 = 0: S4 = 0

FOR I = 0 TO N - 1

2 S1 = S1 + X(I) ^ 2

S2 = S2 + X(I)

S3 = S3 + X(I) * Y(I)

Рекомендуем скачать другие рефераты по теме: древний египет реферат, контроль реферат.



1  2  3  4  5  6 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки