Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

Подставляя его во второе уравнение получаем:  

y = vsin α - .

Сокращая v в первом слагаемом и учитывая, что  = tg α, получаем

уравнение траектории снаряда: y = x tg α – .(8)

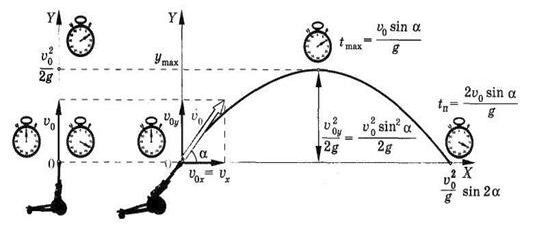
д) Траектория баллистического движения.

Построим баллистическую траекторию (8).

Графиком квадратичной функции, как известно, является парабола. В рассматриваемом случае парабола проходит через начало координат,

так как из (8) следует, что у = 0 при х = 0. Ветви параболы направлены вниз, так как коэффициент ( -  ) при x меньше нуля. (Рис №5).

 (рис №5)

Определим основные параметры баллистического движения: время подъема на максимальную высоту, максимальную высоту, время и дальность полета. Вследствие независимости движений по координатным осям подъем снаряда по вертикали определяется только проекцией начальной скорости  на ось Y. В соответствии с формулой: , полученной для тела, брошенного вверх с начальной скоростью , время подъема снаряда на максимальную высоту равно:

t=  

Максимальная высота подъема может быть рассчитана по формуле ,

если  подставить вместо :

y=

На рисунке №5 сопоставляется вертикальное и криволинейное движение с одинаковой начальной скоростью по оси Y. В любой момент времени тело, брошенное вертикально вверх, и тело, брошенное под углом к горизонту с той же вертикальной проекцией скорости, движутся по оси Y синхронно.

Так как парабола симметрична относительно вершины, то время полета  снаряда в 2 раза больше времени его подъема на максимальную высоту:

t

Подставляя время полета в закон движения по оси X, получаем максимальную дальность полета:

x

Так как 2 sin  cos, а = sin 2, то  

x

е) применение баллистического движения на практике.

Представим себе, что из одной точки выпустили несколько снарядов, под различными углами. Например, первый снаряд под углом 30°, второй под углом 40°, третий под углом 60°,а четвертый под углом 75°(рис № 6).

 

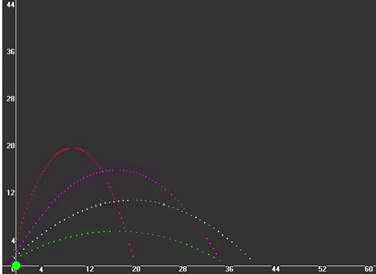
(рис№6) 1)

Рекомендуем скачать другие рефераты по теме: реферат по социологии, скачать сочинение.



Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки