
Бернулли
Категория реферата: Рефераты по математике
Теги реферата: конспекты по истории, сочинение
Добавил(а) на сайт: Mihajlov.
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 | Следующая страница реферата
В 1694 г. в «Асtа Eruditorium» И. Бернулли поместил небольшую статью, в которой упоминалось уравнение тина Риккати. Он писал: «Я еще не выяснил, можно ли разрешить дифференциальное уравнение х2dх + у2dх = d2у». После этой публикации уравнением y’=у2+х2
заинтересовался Я. Бернулли, о чем свидетельствуют его письма Лейбницу в 1697—1704 гг. «Я бы хотел далее от тебя узнать, пытался ли ты исследовать dу=у2dх+х2dх,— писал Я. Бернулли Лейбницу 27 января 1697г.— Я делал множество попыток, но решение этой задачи постоянно ускользало от меня». «Кстати, я вспоминаю другое уравнение dу=у2dх+х2dх,— писал он Лейбницу 15 ноября 1702 г.,— в котором мне не удалось разделить переменные так, чтобы уравнение осталось просто дифференциальным; но я разделил их сведением к следующему дифференциальному уравнению: d2у:у=-х2dx2».
Хотя Я. Бернулли не удалось решить уравнение в конечном виде, интерес к нему у математиков утих. Лишь в 1724 г. граф Джакопо Риккати в Дополнении VIII к «Асtа Eruditorium» поставил задачу: для уравнения у'=ахп+bу2 (а и b — постоянные) найти значения п, при которых оно допускает разделение переменных. Ею занялись Иоганн I, Николай I, Николай II и Даниил Бернулли, но, кроме Даниила, существенных результатов никто не получил.
Д. Риккати свое решение в упомянутом дополнении выразил в виде анаграммы.
В том же выпуске «Асta Eruditorum» была помещена заметка Д. Бернулли, в которой он написал, что уравнение ахndх+ииdх=bdи считается неразрешимым.
Бернулли приступил к исследованию уравнения и вскоре опубликовал свои результаты в «Математических упражнениях». Он установил, что уравнение Риккати допускает интегрирование в конечном виде в случаях n= -4k/(2k±1) (k—целое число).
Случай п=—2 рассмотрел Эйлер. В 1841 г. Лиувилль доказал, что в случаях, отличных от указанных Д. Бернулли и Эйлером, решение уравнения Риккати не сводится к квадратурам и не может быть выражено с помощью конечного числа элементарных функций. Уравнение
у'+а(х)y2+b(x)y+c(x)=0
теперь называют обобщенным уравнением Риккати. Его исследовал Эйлер и установил, что если известно одно частное решение у1(х) уравнения, то подстановка y=y1 (х)+1/и{х) приводит его к линейному. Если же известны два частных решения y1(x) и у2(x), то общий интеграл уравнения находится одной квадратурой.
Интерес к уравнению Риккати объясняется тем, что оно встречается при решении некоторых задач механики; кроме того, к нему можно свести любое линейное уравнение второго порядка.
 Интересы
Д. Бернулли были разнообразны. И вскоре он заинтересовался древней неразрешимой
задачей квадратуры круга просуществовавшей многие века, будоража умы
математиков всех времен. Гиппократ Хиосский (V в. до н. э.) пытался справиться
с квадратурой круга при помощи квадрируемых фигур, ограниченных дугами двух
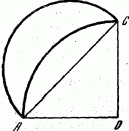
окружностей, названных гиппократовыми луночками. Такую луночку можно, например, построить следующим образом: возьмем четверть круга радиуса r и на хорде АС, соединяющей концы радиусов ОА и ОС, опишем как на диаметре внешнюю по отношению
к четверти круга полуокружность.
Интересы
Д. Бернулли были разнообразны. И вскоре он заинтересовался древней неразрешимой
задачей квадратуры круга просуществовавшей многие века, будоража умы
математиков всех времен. Гиппократ Хиосский (V в. до н. э.) пытался справиться
с квадратурой круга при помощи квадрируемых фигур, ограниченных дугами двух
окружностей, названных гиппократовыми луночками. Такую луночку можно, например, построить следующим образом: возьмем четверть круга радиуса r и на хорде АС, соединяющей концы радиусов ОА и ОС, опишем как на диаметре внешнюю по отношению
к четверти круга полуокружность.
Тогда АС=r√2 и площадь четверти большего круга будет такой же, как площадь меньшего полукруга, т. е. πr2/4.
Пусть S—площадь луночки, S1, S2, S3, S4, —площади соответственно меньшего полукруга, сегмента АС, четверти большего круга, треугольника ОАС. Найдем
S=S1-S2, S2=S3—S4,
поэтому
S= πr2/4- (πr2/4-S4) =S4.
Итак, S=r2/2. Это значит — луночка квадрируема.
Гиппократ получил три квадрируемые луночки. Д. Бернулли в «Математических упражнениях» указал условие, которому должны удовлетворять алгебраически квадрируемые луночки, и привел уравнение, дающее четвертую квадрируемую луночку.
Однако луночки Гиппократа задачу о квадратуре круга вперед к решению не продвинули: в 30—40-х годах XX в. И. Г. Чеботаревым и А. В. Дородновьш доказано, что существует пять видов квадрируемых луночек, но они не квадрируемы вместе с кругом.
Вторая часть «Математических упражнений», посвященная вопросам механики, по объему составляет почти половину книги.
В 1725 г. Д. Бернулли вместе с И. Бернулли получил первую премию на объявленном Парижской академией наук первом конкурсе на тему «О средствах сохранять равномерность водяных или песочных часов на море». Считается, что этот успех исследования по прикладной механике определил постоянный интерес Д. Бернулли к практическим задачам. И 5 июля 1725 г. был подписан контракт, по которому Д. Бернулли предоставлялось место профессора физиологии Петербургской академии наук с жалованьем 800 рублей в год; 27 октября 1725 г. он вместе с братом Николаем II Бернулли, получившим профессуру по кафедре математики с окладом 1000 рублей (самым высоким из всех платившихся академикам—составлял 4% от суммы, отпущенной Петром I на организацию академии), прибыл в Петербург. В духе механистических воззрений XVII—XVIII вв. Д. Бернулли на кафедре анатомии и физиологии намеревался с помощью механикоматиматических методов изучать тайны живой природы. Он хотел открыть «новую эпоху в физиологии» (из письма Гольдбаху от 17 июня 1730 г.). Произошло же совсем иное: открытия Д. Бернулли легли в основу гидродинамики, гидравлики, физиологии; они применяются в геологии, при исследовании динамики звёзд, в других областях точного естествознания.
Уже упоминалось, что 4 декабря 1725 г. на собрании академиков Д. Бернулли сделал сообщение «Возражение Питкарну против его теории о выделении соков в теле животного». На эту же тему через две недели он сделал второй доклад. Впоследствии тематика исследований Д. Бернулли изменилась: он стал изучать движение мышц человека и животных.
В связи с этим встали чисто механические задачи, определившие сообщения Д. Бернулли: «О сложении и разложении сил» (1 февраля 1726 г.), «Геометрические доказательства к рассуждению о сложении сил» (14 июня 1726 г.) и первые публикации в первом томе «Комментариев» Петербургской академии наук (1728) — «Исследование принципов механики и геометрические доказательства относительно сложения и разложения сил», «Опыт новой теории движения мускулов». В этих работах Д. Бернулли развивал идеи, изложенные И. Бернулли в диссертации «О движении мускулов».
Смерть Николая Бернулли омрачила первые годы жизни Д. Бернулли в Петербурге. На заседании Академии наук 1 августа 1726 г. императрица Екатерина I выразила Д. Бернулли свое соболезнование.
Вскоре умерла Екатерина I; пришедший на престол Петр II переехал в Москву, куда отправился и президент академии Блюментрост. Фактическим руководителем академии стал бывший библиотекарь Петра I И. Д. Шумахер, и это не благоприятствовало работе академии.
Рекомендуем скачать другие рефераты по теме: жизнь реферат, реферат по физкультуре.
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 | Следующая страница реферата