Безинерциальные заряды и токи. Гипотеза об эквивалентности 2-х калибровок

Кулигин В.А., Кулигина Г.А., Корнева М.В.

Введение

Исследуя проблемы калибровки уравнений Максвелла [1], [2], мы математически строго доказали следующее.

1. Задача Коши для уравнений в частных производных не имеет единственного решения. Решение зависит от выбора калибровки, т.е. калибровочная инвариантность и градиентная инвариантность в общем случае не имеют места.

2. Предельный переход в уравнениях Максвелла от волновых процессов к квазистатическим при v<<c является незаконным.

3. В силу этого, электромагнитные волны и квазистатические поля заряженных инерциальных частиц (электронов, протонов и т.д.) должны описываться разными группами уравнений. Электромагнитная волна должна удовлетворять волновому уравнению, а квазистатические поля должны описываться уравнением Пуассона.

Поскольку выводы опираются на строгое математическое доказательство и не содержат каких-либо гипотез, они подрывают основы не только классической электродинамики, но и квантовой электродинамики.

В то же время, хорошее согласие уравнений Максвелла с экспериментом (например, прекрасно подтвержденная экспериментом теория антенно-фидерных систем) и ряд важных результатов в квантовой электродинамике требуют поиска объяснения этих фактов.

В настоящей работе показано, что существует условие, при котором имеет место градиентная инвариантность, т.е. эквивалентность кулоновской калибровки и калибровки Лоренца. Рассмотрены также следствия, вытекающие из этого условия.

1. Токи в коаксиальной линии

Первым направлением наших исследований, нацеленным на решение поставленной проблемы, стал анализ различных калибровок уравнений Максвелла и попытки видоизменить эти уравнения так, чтобы сохранить положительные результаты и правильно описать явления. К сожалению, этот путь не привел нас к желаемым результатам.

Второе направление – анализ решений уравнений Максвелла для различных задач электродинамики. Именно этот путь позволил переосмыслить уравнения Максвелла и найти условие, при котором градиентная инвариантность имеет место.

В качестве иллюстрации рассмотрим распространение полей в коаксиальной линии (ТЕМ волна). Когда к линии подключается источник напряжения, между проводниками линии начинает со скоростью света распространяться электромагнитная энергия. Проводник, как известно, можно рассматривать как квазинейтральную систему, в которой заряды электронов и ионов создают суммарное поле, равное нулю при отсутствии сторонних источников полей. В рамках максвелловской теории имеет место закон сохранения заряда. Если заряды возникают (разделяются), то попарно (положительный и отрицательный) без нарушения этого закона.

Мы должны при объяснении процессов принять также во внимание то, что согласно современным воззрениям средняя скорость электронов проводимости в проводнике весьма мала.

Вернемся к полям в коаксиальной линии. Рассмотрим процесс распространения энергии при подключении к линии источника постоянного напряжения. В современной литературе нет ясного объяснения процесса распространения энергии от источника. Мы рассмотрим некоторые варианты.

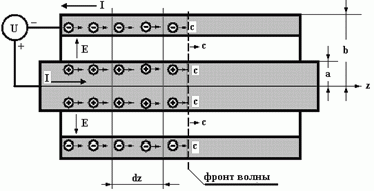
Рис.1

Вариант первый. Это наиболее распространенный вариант объяснения. В линии будет распространяться волна, которая на поверхности проводников образует заряды. Поверхностные заряды движутся и создают поперечное электрическое и магнитное поле.

Однако, если волна возбуждает эти заряды, то они возникают парами в соответствии с законом сохранения заряда (ион и электрон проводимости). Сразу после прохождения фронта волны заряды должны разделяться в обоих проводниках, причем так, чтобы на центральном проводнике существовали и двигались только положительные заряды, а на периферийном – только отрицательные заряды. В противном случае электрическое поле в коаксиальной линии существовать не может! В этом случае мы должны объяснить следующую проблему. Каким образом при рождении пары разноименных зарядов на каждом из проводников (ион и электрон проводимости) электрон проводимости может перескочить с центрального проводника на периферийный, чтобы обеспечить избыток отрицательных зарядов на внешнем проводнике и недостаток – на внутреннем (положительный ион, конечно же, не может!)? Такого механизма перехода не существует.

Вариант второй. Можно предположить другое. Вдоль проводников от источника напряжения и к нему по разным проводникам движутся электроны проводимости как показано на рис. 2. Однако и это положение не согласуется ни с теорией относительности (например, здесь скорость электронов проводимости должна быть равна скорости света), ни с современными представлениями о малой средней скорости перемещения электронов проводимости в проводнике.

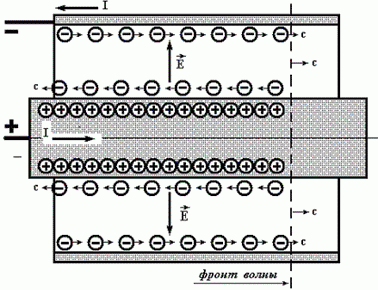
Рис. 2

Третий вариант. Второй вариант объяснения можно дополнить предположением, что электроны проводимости по какой-то причине “теряют” свои инерциальные свойства, т.е. их масса покоя становится равной нулю. Тогда они действительно могут двигаться со скоростью света вдоль поверхности металла. Но и этот вариант имеет дефект. Причина в том, что поверхностные токи на каждом из проводников образуются только электронами проводимости (положительные ионы неподвижны!). Следовательно, при распространении энергии вдоль линии даже при переменном напряжении внутри коаксиальной линии должна образовываться и существовать постоянная составляющая магнитного поля. Экспериментально она не была зафиксирована.

Новый вариант. По этой причине у нас остается единственный вариант объяснения. В проводнике должны существовать положительные и отрицательные заряды, не обладающие инерциальными свойствами. Но это не инерциальные электроны проводимости! Следовательно, не волна возбуждает заряды и токи в коаксиальных линиях, волноводах и т.д. на поверхностях проводников. Такие заряды создаются источником напряжения, и они движутся со скоростью света вдоль поверхности проводников. Именно они порождают в линии электромагнитные поля и переносят энергию; они – источник полей в длинных линиях.

Этот вывод настолько противоречит современным представлениям, что необходимо рассмотреть математическую сторону этого процесса.

Известно, что поля Er и H , которые существуют в коаксиальной линии, образуя ТЕМ волну, удовлетворяют волновым уравнениям.

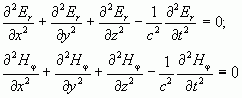(1.1)

Рекомендуем скачать другие рефераты по теме: реферат по обж, курсовая работа на тему бесплатно.



1  2  3  4  5  6 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки