Частные случаи дифференциальных уравнений
Категория реферата: Рефераты по математике
Теги реферата: бесплатные рассказы, решебник по алгебре класс
Добавил(а) на сайт: Николаичев.
Предыдущая страница реферата | 7 8 9 10 11 12 13 14 15 16 17 | Следующая страница реферата
h(t)=k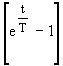
Ч
1(t) (5)
Функцию веса можно получить дифференцированием переходной функции
w(t)=
или из преобразований Лапласа
w(t)=w(s)
w(s)=W(s)Ч 1
W(s)=
= 
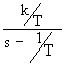
Переходя к оригиналу, получим
w(t)=
e
Ч
1(t) (6)
4. Построим графики переходной функции и функции веса. Подставляя исходные данные, вычислим коэффициент передачи, постоянные времени и временные характеристики:
k=2
T =0.62
h(t)=2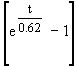
Ч
1(t)
w(t)=3.2e
Ч
1(t)
Переходная функция представляет собой экспоненту. Множитель 1(t) указывает ,что экспонента рассматривается только для положительного времени t>0. Функция веса - также экспонента, но со скачком в точке t=0 на величину
.
5. Получим частотную передаточную функцию, заменив в передаточной функции (4) s на jw :
W(s)= 
W(jw
)=
(7)
W(jw
)=
=
j
=U(w
)+jV(w
)
U(w
)=
V(w
)=
6. Получим аналитические выражения для частотных характеристик. По определению амплитудная частотная характеристика (АЧХ) - это модуль частотной передаточной функции, т.е.
A(w )=Ѕ W(jw )Ѕ
A(w
)=
=
(8)
Фазовая частотная характеристика (ФЧХ) - это аргумент частотной передаточной функции, т.е.
Рекомендуем скачать другие рефераты по теме: первый снег сочинение, реферати українською.
Предыдущая страница реферата | 7 8 9 10 11 12 13 14 15 16 17 | Следующая страница реферата