
Дедукция и индукция
Категория реферата: Рефераты по математике
Теги реферата: новшество, отправить сообщение
Добавил(а) на сайт: Anasenko.
Предыдущая страница реферата | 1 2 3 4 | Следующая страница реферата
а) При n=1 получим a1=a1+d(1-1)=a1. Следовательно формула верна.
б) Пусть k - любое натуральное число и пусть формула справедлива при n=k, то есть
ak=a1+d(k-1).
Докажем, что тогда формула верна и для следующего натурального числа n=k+1, то есть докажем, что
ak+1=a1+d(k).
По определению арифметической прогрессии имеем
ak+1=ak+d.
Подставим в это равенство выражение для ak, которое, согласно предположению индукции, считаем верным. Получим
ak+1=ak+d=a1+d(k-1)+d=a1+d(k).
Значит, формула (1) верна для всех n.
Задача 1. Курс воздушных ванн врачи рекомендуют начинать с 15 мин в 1-й день, а за тем увеличивать время этой процедуры каждый следующий день на 10 мин. Сколько дней следует принимать воздушные ванны в указанном режиме, чтобы достичь их максимальной продолжительности в 1 час 45 мин?
Решение. Продолжительность приёма воздушных ванн в каждый день представляет собой арифметическую прогрессию с первым членом a1=15 мини разностью d=10мин. Спрашивается, в какой день продолжительность достигает 1 час 45 мин, то есть 105 мин? Воспользуемся формулой (1) общего члена арифметической прогрессии:
an=a1+d(n-1)=105.
Отсюда получим
15+10(n-1)=105 или n=10 (дней).
Основное свойство арифметической прогрессии.Последовательность a1, a2, a3, ..., an, ... является арифметической прогрессией тогда и только тогда, когда каждый её член, начиная со второго, равен среднему арифметическому двух соседних с ним членов, то есть
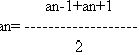
Формулы суммы n первых членов арифметической прогрессии:
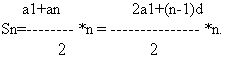
2. Геометрической прогрессией называется последовательность не равных нулю чисел, каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и то же число. Это постоянное число называется знаменателем прогрессии. Члены геометрической прогрессии обозначают через b1, b2, b3, ..., bn, ... , знаменатель прогрессии - через q.
Примеры.1. Числа 5, 10, 20 ,40, ... образуют геометрическую прогрессию со знаменателем q=2 (возрастающую).
2. Числа 1; 0,1; 0,01; 0,001; ... образуют геометрическую прогрессию со знаменателем q=0,1 (убывающую).
3. Числа 3, -6, 12, -24, ... образуют геометрическую прогрессию со знаменателем q=-2 (отметим, что знаменатель может быть любым числом, не равным 0).
Для задания геометрической прогрессии достаточно задать её первый член b1 и её знаменатель q. Любой член геометрической прогрессии можно вычислить по формуле
bn=b1*q^(n-1) (3)
Рекомендуем скачать другие рефераты по теме: рефераты по истории россии, титульный лист курсовой работы.
Предыдущая страница реферата | 1 2 3 4 | Следующая страница реферата