Рефераты | Рефераты по математике | Дисперсионный анализ Дисперсионный анализ Категория реферата: Рефераты по математике Теги реферата: реферат отрасль, реферат электрические Добавил(а) на сайт: Роман. Предыдущая страница реферата | 5  6  7  8  9  10  11  12  13  14  15 | Следующая страница реферата
Межгрупповая (фактор B)		l-1
Взаимодействие		(m-1)(l-1)
Остаточная		mln - ml
Общая		mln - 1

Проверка нулевых гипотез HA, HB, HAB об отсутствии влияния на рассматриваемую переменную факторов А, B и их взаимодействия AB осуществляется сравнением отношений , ,  (для модели I с фиксированными уровнями факторов) или отношений , ,  (для случайной модели II) с соответствующими табличными значениями F – критерия Фишера – Снедекора. Для смешанной модели III проверка гипотез относительно факторов с фиксированными уровнями производится также как и в модели II, а факторов со случайными уровнями – как в модели I.

Если n=1, т.е. при одном наблюдении в ячейке, то не все нулевые гипотезы могут быть проверены так как выпадает компонента Q3 из общей суммы квадратов отклонений, а с ней и средний квадрат , так как в этом случае не может быть речи о взаимодействии факторов.

С точки зрения техники вычислений для нахождения сумм квадратов Q1, Q2, Q3, Q4, Q целесообразнее использовать формулы:

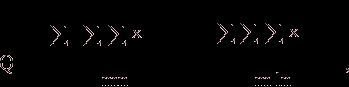
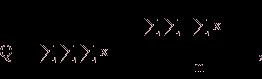
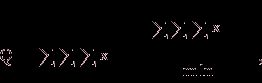
Q3 = Q – Q1 – Q2 – Q4.

Отклонение от основных предпосылок дисперсионного анализа — нормальности распределения исследуемой переменной и равенства дисперсий в ячейках (если оно не чрезмерное) — не сказывается существенно на результатах дисперсионного анализа при равном числе наблюдений в ячейках, но может быть очень чувствительно при неравном их числе. Кроме того, при неравном числе наблюдений в ячейках резко возрастает сложность аппарата дисперсионного анализа. Поэтому рекомендуется планировать схему с равным числом наблюдений в ячейках, а если встречаются недостающие данные, то возмещать их средними значениями других наблюдений в ячейках. При этом, однако, искусственно введенные недостающие данные не следует учитывать при подсчете числа степеней свободы /1/.

Рекомендуем скачать другие рефераты по теме: лечение шпоры, шпаргалки по экономическому.



Предыдущая страница реферата | 5  6  7  8  9  10  11  12  13  14  15 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки