Предыдущая страница реферата | 1  2  3 | Следующая страница реферата

Для вычисления двойного интеграла (6) его нужно заменить повторным. Пусть область интегрирования S определяется неравенствами

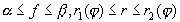
Где r1(j ), r1(j ) - однозначные непрерывные функции на отрезке [a ,b ].

Имеем

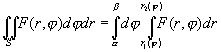(8)

Где

F(r,j ) = rf(r cosj , r sinj )

Пример 1.

Переходя к полярным координатам j и r, вычислить двойной интеграл

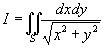
Где S - первая четверть круга радиуса R=1, с центром в точке О(0,0) (рис 3).

Так как

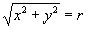то применяя формулу (6), получим

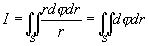
Область S определена неравенствами

Поэтому на основании формулы (8) имеем

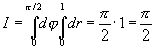
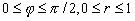
Пример 2.В интеграле

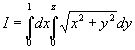(9)

перейти к полярным координатам.

Область интегрирования здесь есть треугольник S, ограниченный прямыми y=0, y=x, x=1

В полярных координатах уравнения этих прямых записываются следующим образом: j =0, j =p /4, r cosj =1 и, следовательно, область S определяется неравенствами

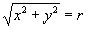
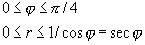
Отсюда на основании формул (6) и(8), учитывая, что имеем

Рекомендуем скачать другие рефераты по теме: рим реферат, образ сочинение.



Предыдущая страница реферата | 1  2  3 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки