Предыдущая страница реферата | 1  2  3 | Следующая страница реферата

Выражение

dS = r dj dr

называется двумерным элементом площади в полярных координатах. Итак, чтобы в двойном интеграле (1) перейти к полярным координатам, достаточно координаты x и y заменить по формулам (2), а вместо элемента площади dS подставить выражение (7).

  

Для вычисления двойного интеграла (6) его нужно заменить повторным. Пусть область интегрирования S определяется неравенствами

Где r1(j), r1(j) - однозначные непрерывные функции на отрезке [a,b]. (рис 2).

Имеем

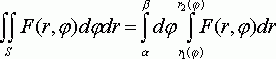   (8)

Где

F(r,j) = rf(r cosj, r sinj)

Пример 1.

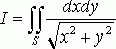Переходя к полярным координатам j и r, вычислить двойной интеграл

Где S - первая четверть круга радиуса R=1, с центром в точке О(0,0) (рис 3).

Так как

то применяя формулу (6),

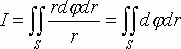
получим

Область S определена

Неравенствами

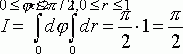
Поэтому на основании формулы (8) имеем

Пример 2.

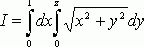В интеграле

   (9)

перейти к полярным координатам.

Область  интегрирования здесь есть треугольник S, ограниченный прямыми y=0, y=x, x=1 (рис 4).

Рекомендуем скачать другие рефераты по теме: изложение язык, реферат на тему функции.



Предыдущая страница реферата | 1  2  3 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки