Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Всякая бесконечно малая последовательность является ограниченной.

Всякая сходящаяся последовательность является ограниченной.

Лучшему прояснению подобных ситуаций может способствовать схематическое изображение неявно сформулированной в рассматриваемых примерах конструкции импликации (схема 1):

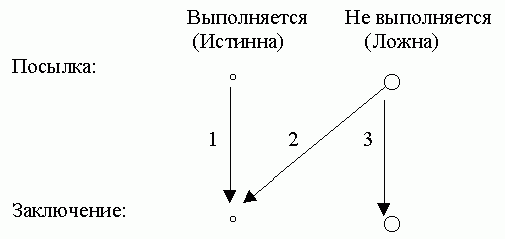
Для теорем, имеющих обратные, возможны ситуации 1 и 3, а для теорем, не имеющих обратных, возможны все три ситуации.

Логическая символика освобождает информацию от непосредственного чувственного познания и создаёт обобщенные формы представлений при изучении математики. Действительно, последние два рассмотренных примера и такие теоремы как: любая дифференцируемая в данной точке функция непрерывна в этой точке, вертикальные углы равны и т.д., выражаются одной и той же логической конструкцией: , в отличие от теорем вида: &. К последним относятся, например, теорема Пифагора, теоремы о пересечении двух прямых третьей, теорема Дезарга о перспективных треугольниках и т.д. Так называемые "теоремы существования" в сущности, выражаются теми же указанными логическими конструкциями. Действительно, предикаты и могут не быть элементарными. Например, если имеет вид: , то получаем формулировку теоремы существования. К теоремам существования вида относится, например, следующая: из всякой ограниченной последовательности можно выделить сходящуюся подпоследовательность.

Используемые в искусственном языке символы составляют аппарат знаковых систем (терминология С.И. Архангельского [3]). Необходимым является не только наличие у студентов навыка применения символических знаков, но и их использование как инструмента познания на уровне автоматизма. Например, процедура нахождения корней характеристического уравнения при решении систем линейных дифференциальных уравнений проводится на основе автоматизированных навыков, без воспроизведения обоснований проводимых действий. Об автоматизированных навыках при использовании знаковых систем С.И. Архангельский пишет: "Характерным признаком развития автоматизированных навыков в применении аппарата знаковых систем, так же как и других навыков, приобретаемых в процессе обучения, является их девербализация, т.е. уменьшение непосредственного обращения ко второй сигнальной системе, к речевому выражению. В то же время при всяком обучении, и особенно при обучении в высшей школе, весьма важно сочетание и параллельное развитие автоматизации навыков в применении знаковых систем, осмысливании и сознательная оценка существа явлений, заключенных в соответствующие формулы, правила, графики и другие выражения" [3, c.209].

Рассмотрим логико-информационные умения. Умению вычленить в информации самое главное можно учить студентов с начала первого курса. В роли главного в разных ситуациях могут выступать различные объекты: части текста; набор нескольких теорем или одна какая-то ведущая теорема раздела; основные понятия и идеи той или иной теории и даже отдельные слова. Например, при изучении основных теорем о счётных множествах необходимо обратить внимание на то, почему в отдельных теоремах за исходные берутся бесконечные множества, а в других - несчётные. Так, присоединяя к бесконечному множеству конечное или счётное, получим множество, эквивалентное исходному; а в теореме об удалении конечного или счётного множества в качестве исходного надо брать уже несчётное множество. Студенты сами должны привести пример, показывающий роль слова "несчётное" во второй теореме. Их рассуждение в простейшем случае может выглядеть следующим образом: удалим из множества чисел натурального ряда все числа, начиная с некоторого -го, т.е. из бесконечного множества удалим счётное вида , где . Останется конечное множество из элементов. Таким образом, при некоторых удалениях из бесконечного счётного множества получаем множество, не эквивалентное исходному. Здесь попутно студенты сами обнаруживают, что при удалении конечного множества из любого бесконечного получается множество, эквивалентное исходному.

Другой пример. Пусть решается следующая задача:

- выпуклый четырёхугольник, и - середины сторон и , соответственно. Доказать, что .

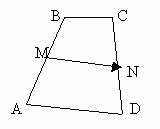
Рисунок 1.

При её решении выясняется, что выпуклость является лишним требованием и четырёхугольник может не быть выпуклым, а например таким, как на рисунках 2 или 3:

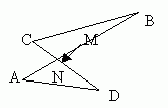
Рисунок 2

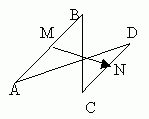
Рисунок 3

Построив на рисунках 2 и 3 отрезки и , получим новые выпуклые четырёхугольники и , и, переобозначив вершины четырёхугольников в естественном порядке, будем иметь две новые задачи а) и б):

а) Доказать, что вектор отрезка, соединяющего соответственно середины диагоналей и четырёхугольника , равен полусумме пар векторов сторон:

б) Вектор средней линии четырёхугольника , где , , равен полусумме векторов и , определяющих его диагонали.

Далее можно заметить, что точки , вообще, могут не принадлежать одной плоскости. Следовательно, имеем новую задачу: - вершины тетраэдра, и - середины противоположных рёбер и , соответственно. Доказать, что . как отрезок, соединяющий середины противоположных рёбер, вызывает естественные ассоциации со средней линией треугольника и, действительно, устремив точку по ребру к точке , получим, что превратится в среднюю линию треугольника и как частный случай предлагаемой задачи получаем теорему о средней линии треугольника. Так, обратив внимание на роль одного слова "выпуклость", приходим к нескольким новым задачам. Вычленение главного в теме можно проводить на заключительном занятии по ней в рамках подведения итогов, которое может осуществляться в форме коллективной мыследеятельности и, частично, проблемно-научного диалога преподавателя с аудиторией.

При изучении теорем и решении задач можно говорить о трёх аспектах представления их доказательства или решения:

логико-символическом - запись теоремы (или задачи) и хода её доказательства (или решения) с использованием символики математической логики;

вербальном (речевом) - инструментом выражения является язык повседневного общения - естественный язык;

Рекомендуем скачать другие рефераты по теме: реферат сша, реферат группы.



Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки