
Геометрия физического пространства
Категория реферата: Рефераты по математике
Теги реферата: онлайн решебник, ответ ру
Добавил(а) на сайт: Якунин.
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 | Следующая страница реферата
почему происходит рождение пары?
что происходит при их аннигиляции?
причем здесь слабые фермионы?
и где же эти вездесущие нейтрино?
Последним вообще как бы не остается места при выше принятой классификации полей. Поиск ответов приводит к смене знаков базиса.
Нет никакого принципиального геометрического (и физического) запрета к смене знаков базиса физического пространства (умножении векторов базиса на –1). Поменяв знаки базиса на противоположные получим комплексное под пространство, сопряженное первому.
В этом случае все становится на место. В сопряженном физическом подпространстве мировые линии частиц (примем для них общее название – «нейтрино») будут располагаться в нашей системе координат согласно рис.3.
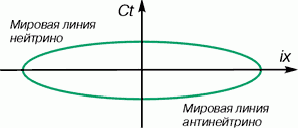
Рис. 3. Мировые линии нейтрино
Смена знаков в уравнениях 2.1.3.1...2.1.3.7 существенно изменит свойства большинства из них, кроме уравнений 2.1.3.1,о котором речь пойдет ниже, и уравнения 2.1.3.2.
В уравнении 2.1.3.2 смена знаков приведет к следующему:
(X1)2 – (X2)2 + (X3)2 = 0 при смене знаков получим:
2.1.3.2*. – (X1)2 + (X2)2 – (X3)2 = 0 или
x2 – e2 + 1 = 0
2.1.3.2.1*. – x2 + e2 – 1 = 0
По сравнению с уравнениями:
– x2 + e2 – 1 = 0
4.3.5.1*. x2 – e2 + 1 = 0 произошла лишь их перестановка.
Это уникальное свойство позволяет им быть единственными взаимодействующими материальными частицами фермионного типа для обоих подпространств. А реакция аннигиляции (и, соответственно, рождения пары) получает свое логическое завершение (см. рис.4).
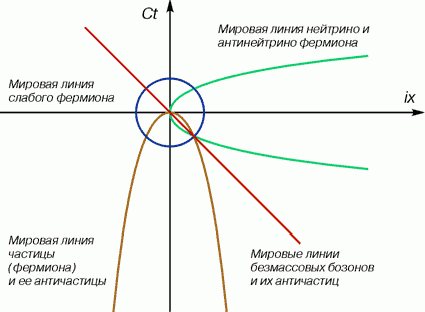
Рис. 4. Реакция аннигиляции. Мировые линии частиц
Получают логическое объяснение все особенности слабых взаимодействий. Как следствие мы можем констатировать, что электрон, позитрон, электронные нейтрино и антинейтрино – суть четыре физические ипостаси одной геометрической сущности. Это же касается и других фермионов.
4.4.7. Поле 2.1.3.1. (Поле Планка)
В отличие от других полей, поле 2.1.3.1 не имеет не скрытых координат, а значит, не наблюдаемо и действует всегда и везде. Так же как и поле слабых фермионов, поле 2.1.3.1 действует в обоих подпространствах. Поле 2.1.3.1 есть закон сохранения в его наиболее общем виде. Поскольку поле определяет кривизну пространства в зависимости от его энергетического состояния, в характеристическое уравнение 2.1.3.1 должна входить постоянная Планка. Группа вращения поля 2.1.3.1 – SU(1, 1). В наблюдаемом подпространстве группа проявит себя как группа U(1), но каждому из множества значений одной переменной будут соответствовать два, противоположных по знаку значения другой переменной.
5. Лирика
Рекомендуем скачать другие рефераты по теме: шпаргалки на экзамен, операции реферат.
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 | Следующая страница реферата