Хроногеометрия несвязных гранично однородных порядков в аффинном пространстве

Н.Л. Шаламова, Омский государственный университет, кафедра математическогомоделирования,

644077 Омск, пр. Мира,55-A

Изучение упорядоченных аффинных пространств An, n>2, связано, как известно, прежде всего с основаниями теории относительности [1]. Следуя же квантовой теории, мы не можем распространять причинно-следственные связи на явления микромира и поэтому вынуждены рассматривать так называемые "несвязные порядки". Предполагая при этом, что скорость передачи взаимодействия и в микромире ограничена, автор получает результаты, изложенные в данной статье.

Рассмотрим в n-мерном аффинном пространстве An, n>2, несвязный порядок , заданный семейством подмножеств An, для которого выполнены условия: (1) ; (2) если , то ; (3) если , то . Несвязность порядка означает, что . Предполагаем далее, что верно следующее: (i) ; (ii) для любой .

Замечание 1. Для любого множества A, будем через , int A, и обозначать соответственно замыкание, внутренность и границу множества A.

Назовем внешним конусом множества Px следующее множество:

где lxy - луч, идущий из точки x и проходящий через точку . Считаем далее, что Cx - конус "с острой вершиной", то есть не содержит прямой. Известным является факт [1], что семейство внешних конусов задает порядок в An.

Гомеоморфизм , для которого f(Px)=Pf(x) для любой точки , назовем порядковым -автоморфизмом. Множество всех порядковых -автоморфизмов будет группой, которую обычно обозначают . Подгруппа группы , сохраняющая фиксированную точку , обозначается .

Порядок называется - однородным или гранично однородным, если для любых найдется такой, что f(x)=y.

Имеет место следующая

Теорема. Пусть , n>2, инвариантной относительно группы параллельных переносов несвязный порядок в n-мерном аффинном пространстве An, для которого выполнены условия:

(1) существует семейство равных и параллельных телесных одинарных замкнутых выпуклых конусов с острой вершиной такое, что для любых и ;

(2) порядок - гранично однородный.

Тогда любой порядковый -автоморфизм будет аффинным преобразованием.

Доказательство .

Для любой точки рассмотрим следующее множество

где объединение берется по всем -автоморфизмам f из стабилизатора таких, что f(v) = uo .

Нетрудно видеть, что , так как тождественное преобразование id, очевидно, принадлежит и для него имеем: id(u0) = u0, и поэтому . В частности, , , так как для любого f(e) = e.

По условию (1) и, кроме того, если , то

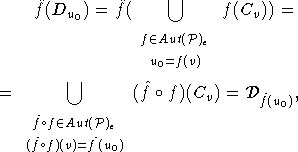
то есть семейство сохраняется -автоморфизмами из .

Замечание 2. Не следует думать, что в определении множества , , f(v) = x точка v- фиксированная. Точка , то есть v- точка из орбиты точки x, для которой определяется множество Dx.

Рассмотрим далее множества

Поделитесь этой записью или добавьте в закладки