Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Отсюда свободная энергия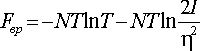             

Таким образом, при рассматриваемых не слишком низких температурах вращательная часть теплоёмкости оказывается постоянной и равной  в соответствии с общими результатами классического рассмотрения. Вращательная часть химической постоянной равна . Существует значительная область температур, в которой выполняется  и в то же время колебательная часть свободной энергии, а вместе с нею и колебательная часть теплоёмкости отсутствуют. В этой области теплоёмкость двухатомного газа равна , т.е. , , а химическая постоянная .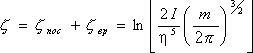

В предельном случае низких температур достаточно сохранить два

первых члена суммы:                       

В том же приближении для свободной энергии:             

Энтропия: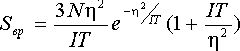                                         

И, наконец, теплоёмкость: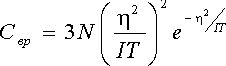

Двухатомный газ с молекулами из

одинаковых атомов. Вращение молекул.

Двухатомные молекулы, состоящие из одинаковых атомов, обладают специфическими особенностями, что приводит к необходимости изменить полученные выше формулы.

Прежде всего, остановимся на высокотемпературном случае в классическом рассмотрении. Благодаря тому, что ядра одинаковы, две взаимно противоположные ориентации оси молекулы соответствуют теперь одному и тому же физическому состоянию молекулы. Поэтому классический статистический интеграл (**) должен быть разделён пополам, и приведёт к изменению химической постоянной, которая теперь равна            .

Исчезнет также и множитель 2 в аргументе логарифма (***).

Фактически этот вопрос нас интересует в применении к изотопам водорода ( и ), и ниже везде будем иметь в виду именно эти газы. Требование квантовомеханической симметрии по ядрам приводит к тому, что у электронного терма  (нормальный терм молекулы водорода) вращательные уровни с чётными и нечётными значениями К обладают различными ядерными кратностями вырождения: уровни с чётными (нечётными) К осуществляются лишь при чётном (нечётном) суммарном спине обоих ядер и имеют относительные кратности вырождения    

                 

при полуцелом спине ядер i , или

                 

при целом i.

Для водорода принята терминология, согласно которой молекулы, находящиеся в состояниях с большим ядерным статистическим весом , называют молекулами ортоводорода, а в состояниях с меньшим весом – молекулами параводорода. Таким образом, для молекул  и  имеем следующие значения статистических весов:

 [орто    , ]                  [    , ]

            В то время как у молекул с различными ядрами ядерные кратности вырождения у всех вращательных уровней одинаковы и потому учёт этого вырождения привёл бы нас к малоинтересному изменению химической постоянной, здесь оно приводит к изменению самого вида статсуммы, которая теперь выглядит так:

,

где

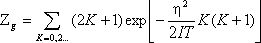
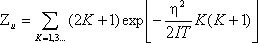
Соответствующим образом изменится свободная энергия

Рекомендуем скачать другие рефераты по теме: проблема дипломной работы, шпаргалки по русскому.



Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки