Индексные числа
Категория реферата: Рефераты по математике
Теги реферата: курсовик, доклады бесплатно
Добавил(а) на сайт: Яскевич.
Предыдущая страница реферата | 11 12 13 14 15 16 17 18 19 20 21 | Следующая страница реферата
117
Рефераты | Рефераты по математике | Индексные числа |
|||
|
S |
551 |
Невзв. индекс =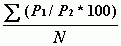 
= 
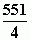=138
Во многих задачах требуется определять индексные числа, исходя из взвешивания в соответствии с важностью (значимостью) того или иного элемента, поэтому более распространенным является метод взвешенных относительных средних. В разделе 3, где подсчитывался взвешенный совокупный ценовой индекс, мы использовали объем потребления продукции в качестве весовых коэффициентов, тогда как в методе взвешенных относительных средних мы используем валовую стоимости каждого элемента группы (это величина получается умножением цены на количество).
Различные способы определения весов. В данном методе существует несколько способов определения взвешенных значений. Как и для индекса Ласпере, мы можем использовать базовую валовую стоимость, полученную умножением базового количества на базовую цену. Использование базовой стоимости приведет нас к тому же результату, что и в случае подсчета индекса по методу Ласпере. Поскольку результат одинаков, то решение об использовании метода Ласпере или метода взвешенных относительных средних часто зависит от возможности получения самих данных. Если более доступными являются данные о стоимости товаров, то используется метод взвешенных относительных средних. Мы применяем индекс Ласпере, если проще и дешевле получить количественные данные.
Подсчет взвешенного индекса относительного среднего:
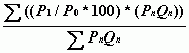(4.9)
PnQn-стоимость;
P1 - цены текущего периода;
P0 - цены базового периода.
Pn и Qn - цены и количества, которые определяют значения, используемые нами как веса. В частности:
n = 0 для базового периода:
n = 1 для текущего периода;
n = 2 для фиксированного периода.
Следовательно, в случае базовых стоимостей формула (3.7) примет вид:
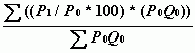(4.10)
Соотношение между данными методом и методом Ласпере: расчет по формуле (4.10) эквивалентен расчету индекса Ласпере для любой задачи.
В особых случаях в общей формуле возможно использование стоимостей, полученных умножением цены из одного периода на количество из другого периода.
Пример: Данные, приведенные в табл.4.13 были взяты из табл.3.9. Поскольку мы имеем цены и количества базового периода, то расчеты будем делать по формуле (4.10). Ценовой индекс, равный 122, немного отличается от 121, полученного в табл.3.7. Расхождение объясняется промежуточными округлениями.
Таблица 4.13 Подсчет взвешенного индекса относительных средних
|
Элементы |
P0 |
P1 |
Q0 |
P1:P0 |
P0Q2 |
Взвеш. относит |
||
|
Совокупного |
Средняя цена (долл.) |
Среднее колич. |
Предыдущая страница реферата | 11 12 13 14 15 16 17 18 19 20 21 | Следующая страница реферата Поделитесь этой записью или добавьте в закладкиКатегории: | |||||