Интеграл по комплексной переменной

Категория реферата: Рефераты по математике
Теги реферата: контрольные работы 7 класс, деньги реферат
Добавил(а) на сайт: Jaskevich.

С помощью формулы (3) можно получить производную любого порядка от аналитической функции  f (Z) в любой точке Z области ее аналитичности. Для доказательства этой теоремы используется формула (2) и соответственные рассуждения, которые привели к ее выводу.

ТЕОРЕМА МОРЕРА. Пусть f(Z) непрерывна в односвязной области G и интеграл от этой функции по любому замкнутому контуру, целиком принадлежащему  G равен 0. Тогда функция f (Z) является аналитической функцией в области G. Эта теорема обобщается и на случай многосвязной области G.

Разложение функции комплексного переменного в ряды.

Если функция f(x, y) определена и непрерывна вместе с частными производными (до n-го порядка ), то существует разложение этой функции в ряд Тейлора :

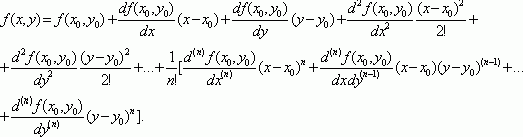
Итак, если задана функция f (z) комплексного переменного, причем f (z) непрерывная вместе с производными до n-го порядка, то:

               (2) – разложение в ряд Тейлора.

Формула (2) записана для всех Z принадлежащих некоторому кругу | Z-Z0 |

Скачали данный реферат: Afinodor, Drjomin, Янзинов, Kruglikov, Jaz'kov, Korjavov.
Последние просмотренные рефераты на тему: реферат по физкультуре, скачати реферат, банк курсовых работ бесплатно, решебник по математике класс виленкин.

Поделитесь этой записью или добавьте в закладки