Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Рис.2: Форма воздушных пузырьков на дне сосуда при различной смачиваемости

Перед тем, как оторваться от дна, пузырек поднимается на конической "ножке" (рис.3а). Поэтому толщина ножки в месте "перетяжки" (согласно нашим наблюдениям около 20 мкм), а не радиус основания определяет размеры отрывающегося пузырька. Зависимость радиуса отрывающегося пузырька от радиуса перетяжки rper:

rkp(rper) = (0.75p0/rв g)1/3 rper2/3 (6)

Диаметр всплывающих пузырьков по расчетам должен быть порядка миллиметра. Наблюдаемые размеры пузырьков были близки к расчетным. Неоднородность смачивания и слияние пузырьков на дне приводили только к увеличению их размеров.

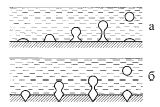
Рис.3: Эволюция пузырька пара на дне: (а) гладкое дно, (б) влияние дефектов

Пузырьки пара

Пузырьки пара образуются, когда температура придонных слоев воды достигает Tkp, при котором давление насыщенных паров в пузырьке больше p [см. (1)]. При T > Tkp пузырьки за счет пара увеличиваются в объеме в десятки раз, и отрывающиеся пузырьки можно считать состоящими только из пара. ПП, как правило, раздуваются в одних и тех же точках дна или поверхности нагревателя, связанных с дефектами (трещинками), ширина которых настолько мала, что в них не попадает вода и постоянно находится воздух (рис.3б) [2]. Эволюция ПП на дне подобна эволюции ВП, но происходит значительно быстрее и скачками.

Подъем пузырьков пара в воде

Скорость подъема оторвавшихся от дна ПП определяется их размерами, видом обтекания и вязкостью воды [2, 3]. Возможны два варианта изменения размеров ПП при всплытии:

1) если вода достаточно прогрета (T > Tkp во всем объеме), то пузырек поднимается с непрерывным увеличением размеров, достигает поверхности и лопается;

2) если T > Tkp только в придонном слое, то увеличение размеров на определенной высоте сменяется уменьшением, и пузырек схлопывается в объеме.

Подъем пузырька с увеличением радиуса

Пусть сферический пузырек поднимается под действием силы Архимеда [2]. Сила сопротивление воды при этом зависит от характера обтекания пузырька водой (рис.4).

При малых размерах наблюдается ламинарное течение: вода течет спокойно, послойно (рис.4а). Для скорости всплытия vлам выполняется формула Стокса:

vлам = Fпод/6phr = 2rвg r2 /9h, (7)

где h - коэффициент вязкости воды. Когда пузырек всплывает с постоянной скоростью, подъемная и тормозящая силы (Fпод и Fторм) равны между собой и Fторм ~ vлам. Для пузырька радиусом около миллиметра скорость всплытия vлам = 2,2 m/c и со дна стакана он должен всплыть за 0.045 c! Очевидно, что это не так. Значит для пузырьков, отрывающихся от дна, формула Стокса не применима. При больших размерах пузырька сзади него образуются пустоты, разрывы и завихрения - наблюдается турбулентное течение (рис.4б). Для такого движения можно получить приближенную формулу [2], определяющую скорость всплытия vтур:

vтур = (8rg/3)1/2. (8)

Если весь объем воды нагрет выше критической температуры, то при подъеме размеры ПП продолжают увеличиваться. Достигнув поверхности, ПП либо сразу прорывает поверхностную пленку, либо некоторое время колеблется и меняет форму, избавляясь от избыточной энергии. Когда пузырек лопается, вся окружающая его жидкость устремляется внутрь, и возникает кольцевая волна. Смыкаясь, она создает кумулятивную струю - выбрасывает вверх столбик воды, от подножья которого распространяется волна (рис.5).

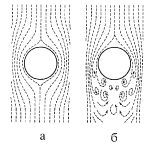
Рис.4: Ламинарное (а) и турбулентное (б) обтекание всплывающего пузырька

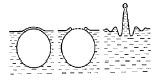
Рис.5: Разрушение пузырька пара на поверхности

Подъем пузырька с уменьшением радиуса

Рекомендуем скачать другие рефераты по теме: налоги в россии, реферат по физике.



Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки