Кластерный анализ
Категория реферата: Рефераты по математике
Теги реферата: сообщение об открытии, здоровый образ реферат
Добавил(а) на сайт: Nilin.
Предыдущая страница реферата | 3 4 5 6 7 8 9 10 11 12 13 | Следующая страница реферата
Рефераты | Рефераты по математике | Кластерный анализ |
100000 |
Довольно часто
критерием объединения (числа кластеров) становится изменение соответствующей
функции. Например, суммы квадратов отклонений: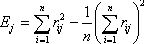 
Процессу группировки должно соответствовать здесь последовательное минимальное возрастание значения критерия E. Наличие резкого скачка в значении E можно интерпретировать как характеристику числа кластеров, объективно существующих в исследуемой совокупности.
Итак, второй способ определения наилучшего числа кластеров сводится к выявлению скачков, определяемых фазовым переходом от сильно связанного к слабосвязанному состоянию объектов.
1.6 Дендограммы.
Наиболее известный метод представления матрицы расстояний или сходства основан на идее дендограммы или диаграммы дерева. Дендограмму можно определить как графическое изображение результатов процесса последовательной кластеризации, которая осуществляется в терминах матрицы расстояний. С помощью дендограммы можно графически или геометрически изобразить процедуру кластеризации при условии, что эта процедура оперирует только с элементами матрицы расстояний или сходства.
Существует много способов построения дендограмм. В дендограмме объекты располагаются вертикально слева, результаты кластеризации – справа. Значения расстояний или сходства, отвечающие строению новых кластеров, изображаются по горизонтальной прямой поверх дендограмм.
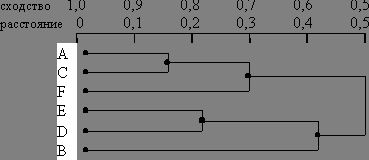
Рис1
На рисунке 1 показан один из примеров дендограммы. Рис 1 соответствует случаю шести объектов (n=6) и k характеристик (признаков). Объекты А и С наиболее близки и поэтому объединяются в один кластер на уровне близости, равном 0,9. Объекты D и Е объединяются при уровне 0,8. Теперь имеем 4 кластера:
(А, С), (F), (D, E), (B).
Далее образуются кластеры (А, С, F) и (E, D, B), соответствующие уровню близости, равному 0,7 и 0,6. Окончательно все объекты группируются в один кластер при уровне 0,5.
Вид дендограммы зависит от выбора меры сходства или расстояния между объектом и кластером и метода кластеризации. Наиболее важным моментом является выбор меры сходства или меры расстояния между объектом и кластером.
Число алгоритмов кластерного анализа слишком велико. Все их можно подразделить на иерархические и неиерархические.
Иерархические алгоритмы связаны с построением дендограмм и делятся на:
а) агломеративные, характеризуемые последовательным объединением исходных элементов и соответствующим уменьшением числа кластеров;
б) дивизимные (делимые), в которых число кластеров возрастает, начиная с одного, в результате чего образуется последовательность расщепляющих групп.
Алгоритмы кластерного анализа имеют сегодня хорошую программную реализацию, которая позволяет решить задачи самой большой размерности.
1.7 Данные
Кластерный анализ можно применять к интервальным данным, частотам, бинарными данным. Важно, чтобы переменные изменялись в сравнимых шкалах.
Неоднородность единиц измерения и вытекающая отсюда невозможность обоснованного выражения значений различных показателей в одном масштабе приводит к тому, что величина расстояний между точками, отражающими положение объектов в пространстве их свойств, оказывается зависящей от произвольно избираемого масштаба. Чтобы устранить неоднородность измерения исходных данных, все их значения предварительно нормируются, т.е. выражаются через отношение этих значений к некоторой величине, отражающей определенные свойства данного показателя. Нормирование исходных данных для кластерного анализа иногда проводится посредством деления исходных величин на среднеквадратичное отклонение соответствующих показателей. Другой способ сводиться к вычислению, так называемого, стандартизованного вклада. Его еще называют Z-вкладом.
Z-вклад показывает, сколько стандартных отклонений отделяет данное наблюдение от среднего значения:
, где xi – значение данного наблюдения, – среднее, S – стандартное отклонение.
Среднее для Z-вкладов является нулевым и стандартное отклонение равно 1.
Стандартизация позволяет сравнивать наблюдения из различных распределений. Если распределение переменной является нормальным (или близким к нормальному), и средняя и дисперсия известны или оцениваются по большим выборным, то Z-вклад для наблюдения обеспечивает более специфическую информацию о его расположении.
Заметим, что методы нормирования означают признание всех признаков равноценными с точки зрения выяснения сходства рассматриваемых объектов. Уже отмечалось, что применительно к экономике признание равноценности различных показателей кажется оправданным отнюдь не всегда. Было бы, желательным наряду с нормированием придать каждому из показателей вес, отражающий его значимость в ходе установления сходств и различий объектов.
В этой ситуации приходится прибегать к способу определения весов отдельных показателей – опросу экспертов. Например, при решении задачи о классификации стран по уровню экономического развития использовались результаты опроса 40 ведущих московских специалистов по проблемам развитых стран по десятибалльной шкале:
Рекомендуем скачать другие рефераты по теме: рефераты, банк рефератов.
Предыдущая страница реферата | 3 4 5 6 7 8 9 10 11 12 13 | Следующая страница реферата