Предыдущая страница реферата | 1  2

Под квадратным корнем здесь оказалось отрицательное число. В то же время имеет решение х = 6 – это легко проверить.

       Однако, предположим на секунду, что корни из отрицательных чисел существуют. Тогда, если научиться извлекать кубические корни из выражения вида А+, можно будет вычислить х= Мы получим 3+ и 3-. В самом деле, возведем в куб выражение 3+, воспользовавшись формулой (a+b)3 = a3 + 3a2b + 3ab2 + b3:

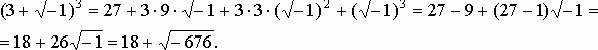
Аналогично,  Поэтому х.

       Как видим, “странные” корни успешно сокращаются. То есть мы решили обычное уравнение и нашли корень – обычное действительное (и даже натуральное) число. Но для этого в промежуточных выкладках нам пришлось оперировать “необычными“ числами. И самое главное – никаким другим способом, за исключением разве что угадывания, это решение получить не удается! 

       Теперь у нас есть три пути:

-      безоговорочно следовать установленным запретам и отказаться от новых приобретений, т.е. считать, что никакого метода решения неприводимого случая кубического уравнения у нас нет;

-      “спрятать голову в песок”, т.е. каждый раз, решая уравнение, при переходе к действию с выражениями вида  говорить “извените!”, а возвращаясь “на законную почву”, делать вид, что ничего не произошло;

-      коль скоро допустили в промежуточные вкладки объекты новой природы, всерьез заняться их изучением: дать определение, исследовать свойства, научиться выполнять арифметические операции.

        Хотя и не сразу, но в конечном итоге математеки выбрали третий путь. И были вознаграждены: “странные” корни нашли широкое применение в электротехнике, аэродинамике и других областях знаний.

       Итак, кроме привычных действительных (буквально – “реально существующих”) чисел нам приходится рассматривать еще числа вида, где А – положительное действительное число. Что за числа, как их “потрогать руками” – все это вопросы, не имеющие ответа. Мы просто договарились считать, что они есть. И вполне естественно, что такие числа были названы мнимыми, т.е. “нереальными”. Сама идея комплексного числа возникла у итальянских математиков XVI в. в процессе решения уравнений 3-й и 4-й степеней.

       Но кое-что о мнимых числах ма все же знаем. Например, что при возведении в квадрат они дают отрицательные числа. Далее, поскольку , то =, а  - это обычное действительное число. Значит, мнимое число можно получить исходя из единственного мнимого числа, если умножить его на подходящее действительное число. Таким образом, вместо безбрежного океана таинственных обьектов мы имеем один-единственный непривычный объект, все же остальные строятся с помощью операции умножения. Согласитесь, с такой ситуацией примерится уже гораздо легче.

       Число , играющее роль “строительного блока” в мире мнимых чисел, называют мнимой единицей и по предложению Леонардо Эйлера обозначают i (от лат. imaginarius – “мнимый”), но формальные операции над комплексными числами ввел Бомбелли. Основное свойство мнимой единицы выражается простым равенством:

.

       Однако, как подсказывает опыт решения кубических уравнений, кроме действительных и мнимых нам приходится рассматривать также числа вида А+, которые представляют собой сумму действительного. Такие числа именуются комплексными, т.е. составными.

       А теперь, суммируя все сказанное, сформулируем наконец определение комплексного числа: комплексным числом называется выражение вида a+bi, где a и b – действительные числа, а i – мнимая единица.

Список использованной литературы

В. Антонов. Энциклопедия для детей. Том 11. Математика –

Москва: изд-во “Аванта+”, 1998. – 688 с.

Скачали данный реферат: Булдаков, Листунов, Танков, Ржевский, Ковшутин, Янченко.
Последние просмотренные рефераты на тему: предмет культурологии, менеджмент, варианты ответов, изложение язык.



Предыдущая страница реферата | 1  2

Поделитесь этой записью или добавьте в закладки