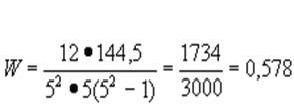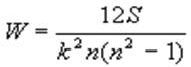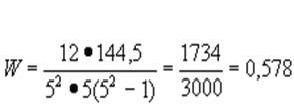Рефераты | Рефераты по математике | Корреляционный анализ для ранговых шкал |
||||
|
Позиция 6 |
1 |
6 |
13 |
6 |
Кроме того, характер парных корреляций не учитывает размера группы. Если Ваши расчеты не автоматизированы, а в программу ЭВМ не заложено ограничение на численность группы, то “умная” машина может абсурдно проранжировать группу из одного человека, присвоив отмеченной одиночной позиции ранг №1, а всем остальным - срединный (для примера табл. 5 это был бы номер 4- срединный между второй и шестой позициями).
Однако, прежде чем делать выводы относительно тесноты парных связей подгрупп (и гомогенности группы в целом), необходима проверка значимости коэффициента, установления того “порогового барьера” a , за которым мы можем говорить о наличии занчимой корреляции. По приведенной выше формуле расчета t находим, что для групп предпринимателей и пенсионеров (r =0,125), значение t равно:
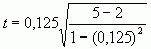= 0,216
что в несколько раз меньше критического (2,353 для a =0,1 и 1,638 для a =0,2). В такой ситуации остается лишь признать связь рядов статистически малозначимой и сильно завысить степень возможной ошибки при повторных замерах (a =0,4-0,5).
В заключение остановимся еще на одном коэффециенте ранговой корреляции, не менее употребимом, чем r . Это множественный коэффициент корреляции W, или, как его еще часто называют, коэффициент конкордации. Предназначаемый, как и r , для измерения степени связи ранжированных переменных, он основывается на несколько иной логике анализа. Если коэффициент Спирмена предназначается для анализа степени совпадения/расхождения отдельных групп, составояющих выборочную совокупность, то для коэффициента W объектом оценивания является, как правило, согласованность мнений всей выборочной совокупности. В первом случае употребляется индуктивный метод анализа - от частных фактов (отдельные подгруппы) к общему умозаключяению (степень гомогенности выборочной совокупности). Коэффициент W используется тогда, когда задачи, гипотезы исследования требуют обратного дедуктивного движения. Например, по 5-7 вопросам анкеты расчитывается коэффициент W. Наименьшие значения W свидетельствуют о максимуме расхождения мнения в подгруппах; спускаясь от общего к частному, исследователь выделяет те подгруппы, которые внесли наибольший диссонанс в общую картину и выдвигает гипотезы относительно причин данной ситуации.
Коэффициент W, подобно r , принимает значения от -1 до +1 и рассчитывается по формуле:
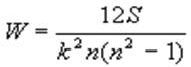
где k - число переменных, n- число ранжируемых позиций,
S- сумма сумм рангов по строке минус среднее, возведенных в квадрат.
Рассмотрим применение W на том- же примере, что и r :
Среднее из суммы рангов равно 75 : 5 = 15. Значение S соответственно будет равно
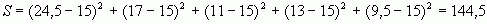. Отсюда
|
|
Рабочие |
Крестья не |
ИТР, слу жащие |
Предпри нимате-ли |
Пенсио-неры |
Предыдущая страница реферата | 2 3 4 5 6 7 8 9 10 11 12 | Следующая страница реферата Поделитесь этой записью или добавьте в закладкиКатегории: |
