Предыдущая страница реферата | 1  2  3

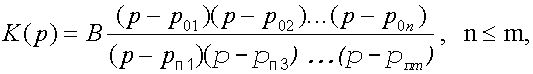
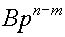
которое при Ѕ pЅ можно представить в виде (под В подразумевается постоянный коэффициент, а p0i и pпi - соответственно нули и полюсы функции К(р)).

Совершенно аналогично и функцию Н(р) при Ѕ pЅ можно представить в форме H(p) = Apn-m где n и m - числа соответственно нулей и полюсов функции Н(р).

При n < m и Ѕ pЅ модуль функции H(p) на полуокружности R ® равен нулю. Таким образом, полуокружность бесконечно большого радиуса R на плоскости р преобразуется в точку, лежащую в начале координат на плоскости Н, и для построения годографа Н в виде замкнутого контура достаточно знать поведение Н(р) на оси iw, то есть знать АЧХ и ФЧХ цепи Ky(iw),Koc(iw).

Обходу контура на рисунке 1 в положительном направлении (против часовой стрелки) соответствует обход годографа Н при изменении частоты от Ґ до -Ґ , т.е. также против часовой стрелки (см. рисунок 3).

Следовательно, если годограф передаточной функции разорванного кольца не охватывает точку 1,i0 , то при замкнутой цепи обратной связи система устойчива, в противном случае система неустойчива.

Это условие называют критерием устойчивости Найквиста, а годограф H(iw) - диаграммой Найквиста.

Показанная на рисунке 3 диаграмма соответствует устойчивой системе. Это видно из того, что годограф Н не охватывает точку 1,i0. Сплошной линией показана часть контура, соответствующая положительным частотам 0<w<Ґ , а штриховой - часть контура, соответствующая отрицательным частотам. Так как функция u(w) четная, а v(w) нечетная относительно w, то оба годографа симметричны относительно действительной оси.

Рисунок 3 был построен для случая, когда при w = 0 передаточная функция Н(iw) отлична от нуля ( эта возможно, например, для усилителей постоянного тока, в которых отсутствуют разделительные конденсаторы).

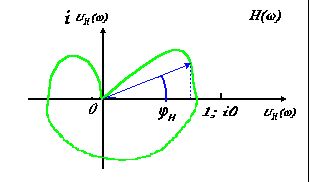
Рисунок 4

Пример диаграммы Найквиста для неустойчивой системы приведена на рисунке 4.

Основное преимущество данного метода : удобство оперирования с АЧХ и ФЧХ разомкнутой цепи.

Следует отметить, что при сложной схеме устройства форма диаграммы бывает настолько усложнена, что по ней сложно судить о попадании точки 1,i0 в замкнутый контур годографа. В подобных случаях оказывается полезным критерий, вытекающий из критерия Найквиста, основанный на подсчете числа пересечений годографом оси Uн(w) на участке 1,Ґ .

Для устойчивости системы тогда необходимо, чтобы годограф либо вообще не пересекал этот отрезок (так, как показано на рисунке 4), либо пересекал его в положительном и отрицательном направлениях одинаковое число раз

* * *

Справедливости ради необходимо заметить, что известны и другие геометрические методы исследования устойчивости линейных систем с обратной связью, например критерий Михайлова и критерий пересечений. Они широко применяются при анализе систем автоматического регулирования. Но мы не будем рассматривать их в данной работе , а при необходимости , с ними можно познакомиться в книге : Котельников В.А., Николаев А.М. “Основы радиоэлектроники”

Литература

1. С.И. Баскаков “Радиотехнические цепи и cигналы” , 1983. М.: Высшая школа.

2. И.С. Гоноровский “Радиотехнические цепи и сигналы”, 1986 М.: Радио и связь.

Скачали данный реферат: Kasperskij, Majstruk, Никифоров, Марин, Прибылов, Kvaskov.
Последние просмотренные рефераты на тему: сочинение евгений онегин, оформление титульный реферата, создание реферата, купить дипломную работу.



Предыдущая страница реферата | 1  2  3

Поделитесь этой записью или добавьте в закладки