2.
Применим (1.5) к интегралам в (1.3), вычислим полученные равенства по формулам
[3, (7.113), (8.108)] и, учитывая (1.1), получим в переменных (x,y):
|
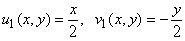
|
(1.6)
|
3.
Соотношения (1.4) в декартовых координатах принимают вид:
|
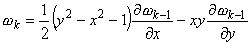
|
(1.7)
|
Из
(1.6)-(1.7), используя индукцию по k, заключаем, что функции uk(x,y) и vk(x,y)
- это гармонические полиномы степени k.
4.
Полиномы uk(x,y) четны по y, а vk(x,y) нечетны. Кроме того, при всех k2
в угловых точках полиномы обращаются в нуль.
5.
Последовательность {uk,vk}Ґk = 1 полна в W(S) и образует в нем базис.
2. Ортогонализация последовательности полиномов
Последовательность
{uk,vk}Ґk = 1 ортогонализуем в скалярном произведении:
|
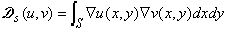
|
(2.1)
|
g№0.
Для того чтобы эта задача была решена при помощи хорошо известного процесса
Грама-Шмидта, необходимо уметь вычислять скалярные произведения вида 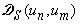 ,
, 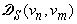 и
и 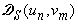 . Если
воспользуемся формулой Грина, то значения этих скалярных произведений дают
следующие формулы:
. Если
воспользуемся формулой Грина, то значения этих скалярных произведений дают
следующие формулы:
где
=j, j = 1,2. Следовательно, можно ортогонализовать
полиномы uk и vk методом Грама-Шмидта в смысле скалярного произведения (2.1).
Получившийся базис будем обозначать как {ek,fk}.
3. Канонический базис
Для
дальнейших результатов нам понадобится новый базис W(S), обладающий
кроме ортогональности еще некоторыми дополнительными свойствами. Так как
ортогональных базисов в гильбертовом пространстве W(S) существует
бесконечно много, то любой из них можно получить из последовательности {ek,fk}
унитарным преобразованием с матрицей перехода Т. Воспользуемся этим и
трансформируем наш базис в базис {l}, ортогональный не только в W(S), но и в следующем скалярном произведении:
где
KR(x0,y0) - шар с центром в (x0,y0) и радиуса R, равного расстоянию от центра
до границы S. Базис с таким дополнительным свойством назовем каноническим в
точке (x0,y0). Доказано (см.[4]), что базис в W(S), канонический в
точке (x0,y0), существует.
Вектор-столбец
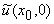 бесконечной
высоты с координатами:
бесконечной
высоты с координатами:

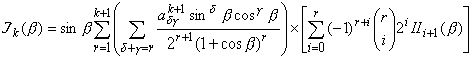
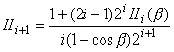
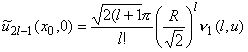 ,
, 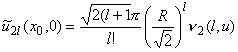 , где
, где