Рефераты | Рефераты по математике | Квантовый эффект Холла в двумерных системах Квантовый эффект Холла в двумерных системах Категория реферата: Рефераты по математике Теги реферата: белорусские рефераты, доклады 7 класс Добавил(а) на сайт: Туполев. Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата p(h/2p)

.

Если подставить численные значения параметров e = 1.6 ·10-19 Кл, B = 102 Тл, (h/2p) = 1.05 ·10-34 Дж·с, то получается, что на каждом уровне Ландау может разместиться примерно 1012 электронов на каждый квадратный сантиметр площади канала.

Полученный результат нуждается в некоторой коррекции. Дело в том, что мы подсчитали число электронов на уровне Ландау с учетом спина, который может принимать два значения: ±1/2. Но в действительности в сильном магнитном поле каждый уровень Ландау расщепляется на два спиновых подуровня, на каждом из которых может разместиться в два раза меньше электронов, чем мы только что подсчитали, а именно:

(здесь и далее h = 2p(h/2p)). Это расщепление уровней достаточно велико, так что спиновые подуровни совершенно не перекрываются. Учет спинового расщепления уровней Ландау не дает ничего нового при рассмотрении квантового эффекта Холла, поэтому мы в дальнейшем будем говорить об уровнях Ландау, хотя на самом деле речь всегда будет идти о подуровне с определенной ориентацией спина.

Проводимость и эффект Холла в двумерном металле

Рассмотрим теперь проводимость и эффект Холла двумерного металла в квантующем магнитном поле. Схема проведения эксперимента представлена на рисунке.

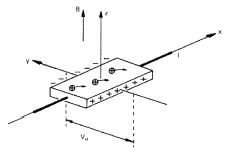
Схема измерения продольного сопротивления и квантового эффекта Холла

Из приведенного рисунка следует, что если пропускать по образцу электрический ток вдоль оси Х, то в магнитном поле Bz ориентированном вдоль оси Z в классическом случае возникает сила Лоренца, отклоняющая электроны к дальней от нас грани образца. Поскольку электроны имеют заряд, то перераспределение электронов вызовет появление электрического поля Ey, величину которого можно найти из условия равенства сил, действующих на электроны в Y-направлении со стороны электрического и магнитного полей: enEy = en vd B, где vd - дрейфовая скорость электрона, n - число электронов проводимости в канале. Величина дрейфовой скорости vd имеет смысл средней скорости направленного движения электронов вдоль оси X и ее не нужно путать со средней скоростью теплового движения.

Учитывая, что плотность электрического тока J = envd, можно получить простое выражение для холловского поля Ey = RJB, где R = 1/(en) - константа Холла. Удобно наряду с константой Холла ввести холловское сопротивление RH = R B. Из определения холловского сопротивления следует, что Ey = RHJ; эта величина действительно измеряется в омах и для случая, когда применима классическая механика, должна быть обратно пропорциональна числу электронов.

Из определения холловского сопротивления следует, что величина RH пропорциональна B и график зависимости RH(B) должен иметь вид прямой линии, выходящей из начала координат, тангенс угла наклона которой к оси абсцисс равен 1/en. Для нормального трехмерного металла при комнатной температуре и не слишком высоких значениях магнитного поля (1-5 Тл) экспериментальные результаты вполне хорошо соответствуют описанной выше картине поведения холловского сопротивления (кстати, эффект Холла в металлах был открыт более ста лет назад в 1879 году американским физиком Е.Г. Холлом).

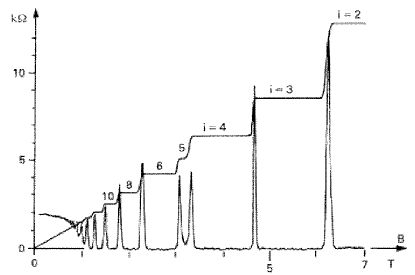
Зависимость холловского сопротивления от величины приложенного магнитного поля. Кривая с острыми пиками - это зависимость омического сопротивления образца от магнитного поля. Как следует из графика, сопротивление каждый раз обращается в нуль, когда квантовый эффект Холла выходит на плато

Экспериментальные результаты, представленные на рисунке, дают совершенно другой результат. Дело в том, что эти опыты проводились в двумерной МОП-структуре при температуре 1 К, когда классическое рассмотрение неприменимо и нужно учитывать квантование движения электронов. Холловское сопротивление обнаруживает ряд ярко выраженных ступенек, причем значение сопротивления для этих ступенек строго определяется выражением RH = h/(ie2), где i = 1,2,3... (на рисунке видны ступеньки со второй по десятую; константа h/e2 примерно равна 25 кОм). Величина Холловского сопротивления оказывается настолько стабильной (не зависящей от параметров образца и температуры), что это позволило использовать ее в качестве национального стандарта электрического сопротивления в целом ряде развитых стран мира.

Попробуем разобраться, почему получается столь странная зависимость холловского и омического сопротивлений от магнитного поля. Будем считать, что полное число электронов в канале фиксировано и напряжение на затворе постоянно. В этом случае максимальная энергия EF, которую имеют электроны проводимости в кристалле (иначе эту энергию называют энергией Ферми), практически не зависит от магнитного поля, если (h/2p)W << EF, а расстояние между уровнями Ландау (h/2p)W прямо пропорционально B и будет линейно уменьшаться при уменьшении B.

Для нашего случая это значит, что если при B = 7 Тл электроны размещались на первом и втором уровнях Ландау, то при B = 5 Тл электроны разместятся уже на трех уровнях Ландау. Иначе говоря, при уменьшении магнитного поля уровни Ландау поочередно пересекают уровень Ферми. При уменьшении магнитного поля полное число электронов не изменилось, а количество электронов, которые могут разместиться на одном уровне Ландау стало меньше (это число одинаково для всех уровней Ландау, лежащих ниже уровня Ферми) в полном соответствии с формулой (2). Поэтому теперь для размещения всех электронов потребовалось занять следующий уровень энергии. Ясно, что если под уровнем Ферми находится точно i полностью заполненных уровней Ландау, то n = ine и если подставить значение ne из формулы (2), то получаем выражение n = i eB/h, которое уже позволяет объяснить численное значение величины квантового эффекта Холла.

Действительно, поскольку B = nh/(ie) и RH = RB имеем, что

Поделитесь этой записью или добавьте в закладки