
–Ь–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–µ –Є –Ї–Њ–Љ–њ—М—О—В–µ—А–љ–Њ–µ –Љ–Њ–і–µ–ї–Є—А–Њ–≤–∞–љ–Є–µ –њ—А–Њ–і—Г–Ї—В–Є–≤–љ–Њ—Б—В–Є —А–∞—Б—В–µ–љ–Є–є –≤ –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є –Њ—В –і–Є–љ–∞–Љ–Є–Ї–Є –≤–ї–∞–ґ–љ–Њ—Б—В–Є –њ–Њ—З–≤—Л
–Ъ–∞—В–µ–≥–Њ—А–Є—П —А–µ—Д–µ—А–∞—В–∞: –†–µ—Д–µ—А–∞—В—Л –њ–Њ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–µ
–Ґ–µ–≥–Є —А–µ—Д–µ—А–∞—В–∞: –Ї—Г–њ–ї—О –і–Є–њ–ї–Њ–Љ–љ—Г—О —А–∞–±–Њ—В—Г, —И–њ–Њ—А—Л –±–µ—Б–њ–ї–∞—В–љ–Њ
–Ф–Њ–±–∞–≤–Є–ї(–∞) –љ–∞ —Б–∞–є—В: Bogun.
–Я—А–µ–і—Л–і—Г—Й–∞—П —Б—В—А–∞–љ–Є—Ж–∞ —А–µ—Д–µ—А–∞—В–∞ | 1 2 3 4 5 6 7 8 9 | –°–ї–µ–і—Г—О—Й–∞—П —Б—В—А–∞–љ–Є—Ж–∞ —А–µ—Д–µ—А–∞—В–∞
–° —Г—З–µ—В–Њ–Љ —Г—А–∞–≤–љ–µ–љ–Є–є (1) вАФ (4) –Є–Љ–µ–µ–Љ —Б–ї–µ–і—Г—О—Й—Г—О –Љ–Њ–і–µ–ї—М —А–∞—Б—З–µ—В–∞ –≤–ї–∞–ґ–љ–Њ—Б—В–Є –њ–Њ—З–≤—Л —Б —Г—З–µ—В–Њ–Љ –і–Є–љ–∞–Љ–Є–Ї–Є –љ–∞–Ї–∞–њ–ї–Є–≤–∞–µ–Љ–Њ–є –±–Є–Њ–Љ–∞—Б—Б—Л:
W (t) = q(t)P(t) + P1(t) вАФ E(t) вАФ H(t),
(7)
E1 (t) =[ (t) вАФ (t)x(t) + b(t)]x(t)/a(t),
–Ш–Ј (4), (5) –Є (6) –Є–Љ–µ–µ–Љ:
b(t) = (1-e1)F(t)/x(t) вАФ ( (t) вАФ (t)x(t))/e0, (8)
–Ф–ї—П –љ–∞—Е–Њ–ґ–і–µ–љ–Є—П –≤–ї–∞–ґ–љ–Њ—Б—В–Є –њ–Њ—З–≤—Л –љ–∞–Љ –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –Є–і–µ–љ—В–Є—Д–Є—Ж–Є—А–Њ–≤–∞—В—М –њ–µ—А–µ–Љ–µ–љ–љ—Л–µ –Є . –≠—В–∞ –Ј–∞–і–∞—З–∞ –і–Њ—Б—В–∞—В–Њ—З–љ–Њ —Б–ї–Њ–ґ–љ–∞ –Є–Ј-–Ј–∞ —Б–ї–Њ–ґ–љ–Њ—Б—В–Є –Є –і–Њ—А–Њ–≥–Њ–≤–Є–Ј–љ—Л –њ—А–Њ–≤–µ–і–µ–љ–Є—П —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞–ї—М–љ—Л—Е –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є–є (–Љ–Њ–љ–Є—В–Њ—А–Є–љ–≥–∞). –Ь—Л –њ—А–Њ–і–µ–Љ–Њ–љ—Б—В—А–Є—А—Г–µ–Љ –Є–Љ–Є—В–∞—Ж–Є–Њ–љ–љ—Г—О –њ—А–Њ—Ж–µ–і—Г—А—Г –µ—С —А–µ—И–µ–љ–Є—П –і–ї—П —Б–ї—Г—З–∞—П –њ–Њ—Б—В–Њ—П–љ–љ—Л—Е –њ–∞—А–∞–Љ–µ—В—А–Њ–≤ –Љ–Њ–і–µ–ї–Є (4); —Б–ї—Г—З–∞–є –Ї—Г—Б–Њ—З–љ–Њ-–њ–Њ—Б—В–Њ—П–љ–љ—Л—Е –њ–∞—А–∞–Љ–µ—В—А–Њ–≤ - –∞–љ–∞–ї–Њ–≥–Є—З–µ–љ –Є –≤–ї–Є—П–µ—В —В–Њ–ї—М–Ї–Њ –љ–∞ —А–∞–Ј–Љ–µ—А–љ–Њ—Б—В—М –Ј–∞–і–∞—З–Є, –∞ —Б–ї—Г—З–∞–є –њ—А–Њ–Є–Ј–≤–Њ–ї—М–љ—Л—Е —Д—Г–љ–Ї—Ж–Є–Є —Б–≤–Њ–і–Є–Љ –Ї –њ—А–Њ–±–ї–µ–Љ–µ –∞–њ–њ—А–Њ–Ї—Б–Є–Љ–∞—Ж–Є–Є –Є—Е –љ–µ–Ї–Њ—В–Њ—А–Њ–є —Б–Є—Б—В–µ–Љ–Њ–є –±–∞–Ј–Є—Б–љ—Л—Е —Д—Г–љ–Ї—Ж–Є–є.
–†–µ—И–µ–љ–Є–µ —Г—А–∞–≤–љ–µ–љ–Є—П (4), –Ї–∞–Ї –ї–µ–≥–Ї–Њ –њ—А–Њ–≤–µ—А–Є—В—М, –Є–Љ–µ–µ—В –≤–Є–і:
x(t)=
/( + Ce вАФ t)![]() . (9)
. (9)
–Ґ–µ–њ–µ—А—М –і–ї—П —В–Њ–≥–Њ, —З—В–Њ–±—Л –љ–∞–є—В–Є –Є –љ—Г–ґ–љ–Њ, —Б–Њ–≥–ї–∞—Б–љ–Њ –Љ–µ—В–Њ–і–∞ –љ–∞–Є–Љ–µ–љ—М—И–Є—Е –Ї–≤–∞–і—А–∞—В–Њ–≤, —А–µ—И–Є—В—М –Ј–∞–і–∞—З—Г –Љ–Є–љ–Є–Љ–Є–Ј–∞—Ж–Є–Є –Ї–≤–∞–і—А–∞—В–Є—З–љ–Њ–≥–Њ —Д—Г–љ–Ї—Ж–Є–Њ–љ–∞–ї–∞ –≤–Є–і–∞:
n
f( , , c) = (xi0 вАФ xi)2 min, (10)
i=1
–≥–і–µ i - –љ–Њ–Љ–µ—А —Д–∞–Ј—Л –≤–µ–≥–µ—В–∞—Ж–Є–Є —А–∞—Б—В–µ–љ–Є—П (i=1,2,...,n); n - —З–Є—Б–ї–Њ —Д–∞–Ј –≤–µ–≥–µ—В–∞—Ж–Є–Є; xi0 - —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞–ї—М–љ—Л–µ –≤–µ–ї–Є—З–Є–љ—Л —Г—А–Њ–ґ–∞–є–љ–Њ—Б—В–Є –Ї—Г–ї—М—В—Г—А—Л –Ј–∞ —А–µ–њ—А–µ–Ј–µ–љ—В–∞—В–Є–≤–љ—Л–є –њ–µ—А–Є–Њ–і –≤—А–µ–Љ–µ–љ–Є; xi - —В–µ–Њ—А–µ—В–Є—З–µ—Б–Ї–Є–µ –≤–µ–ї–Є—З–Є–љ—Л —Г—А–Њ–ґ–∞–є–љ–Њ—Б—В–Є —Б–µ–ї—М—Е–Њ–Ј–Ї—Г–ї—М—В—Г—А, –Њ–њ—А–µ–і–µ–ї—П–µ–Љ—Л–µ –њ–Њ —Д–Њ—А–Љ—Г–ї–µ (9).
–Ф–ї—П –љ–∞—Е–Њ–ґ–і–µ–љ–Є—П —А–µ—И–µ–љ–Є—П –Ј–∞–і–∞—З–Є (10) –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ —А–µ—И–Є—В—М –љ–µ–ї–Є–љ–µ–є–љ—Г—О —Б–Є—Б—В–µ–Љ—Г —Г—А–∞–≤–љ–µ–љ–Є–є:
df / d =0, df / d = 0, df / dc = 0. (11)
–†–µ—И–∞–µ–Љ —Н—В—Г —Б–Є—Б—В–µ–Љ—Г —З–Є—Б–ї–µ–љ–љ–Њ (–љ–∞–њ—А–Є–Љ–µ—А, –Љ–µ—В–Њ–і–Њ–Љ –Ч–µ–є–і–µ–ї—П), —Б —В—А–µ–±—Г–µ–Љ–Њ–є —В–Њ—З–љ–Њ—Б—В—М—О –Є –Ї—А–Є—В–µ—А–Є–µ–Љ –∞–і–µ–Ї–≤–∞—В–љ–Њ—Б—В–Є –≤–Є–і–∞:
( i+1 вАФ i)2 + ( i+1 вАФ i)2 + (—Бi+1 вАФ —Бi)2 < 2 .
–Т–µ–ї–Є—З–Є–љ–∞ —Д–Њ—В–Њ—Б–Є–љ—В–µ–Ј–∞ –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П –њ–Њ —Д–Њ—А–Љ—Г–ї–µ –≤–Є–і–∞:
F(t)=Fmax e вАФ [s(t) вАФ z][ (t)x(t)/ (t)]2/3,
–≥–і–µ s(t) вАФ —В–µ–Ї—Г—Й–∞—П —Б—Г–Љ–Љ–∞ –±–Є–Њ–ї–Њ–≥–Є—З–µ—Б–Ї–Є –∞–Ї—В–Є–≤–љ—Л—Е —В–µ–Љ–њ–µ—А–∞—В—Г—А, z вАФ —Б—Г–Љ–Љ–∞ –±–Є–Њ–ї–Њ–≥–Є—З–µ—Б–Ї–Є –∞–Ї—В–Є–≤–љ—Л—Е —В–µ–Љ–њ–µ—А–∞—В—Г—А –і–ї—П –Љ–∞–Ї—Б–Є–Љ–∞–ї—М–љ–Њ–≥–Њ —А–∞–Ј–≤–Є—В–Є—П –ї–Є—Б—В–Њ–≤–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є, вАФ —Н–Љ–њ–Є—А–Є—З–µ—Б–Ї–Є–є –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В, –Ј–∞–≤–Є—Б—П—Й–Є–є –Њ—В .
–Ю–і–љ–Є–Љ –Є–Ј –љ–∞–Є–±–Њ–ї–µ–µ –≤–∞–ґ–љ—Л—Е —Г—Б–ї–Њ–≤–Є–є —Г–≤–µ–ї–Є—З–µ–љ–Є—П —Г—А–Њ–ґ–∞–є–љ–Њ—Б—В–Є —Б–µ–ї—М—Б–Ї–Њ—Е–Њ–Ј—П–є—Б—В–≤–µ–љ–љ—Л—Е –Ї—Г–ї—М—В—Г—А —П–≤–ї—П–µ—В—Б—П –і–Њ—Б—В–Є–ґ–µ–љ–Є–µ —В–∞–Ї–Њ–≥–Њ —Г—А–Њ–≤–љ—П —Д–∞–Ї—В–Њ—А–∞ —А–Њ—Б—В–∞, –Ї–∞–Ї –≤–ї–∞–ґ–љ–Њ—Б—В—М –њ–Њ—З–≤—Л, –Ї–Њ—В–Њ—А—Л–є –њ–Њ–Ј–≤–Њ–ї–Є—В –њ–Њ–ї—Г—З–Є—В—М –Њ–њ—В–Є–Љ–∞–ї—М–љ—Л–є —А–µ–ґ–Є–Љ –Њ—А–Њ—И–µ–љ–Є—П –Є, –Ї–∞–Ї —Б–ї–µ–і—Б—В–≤–Є–µ, –≤—Л—Б–Њ–Ї–Є–є —Г—А–Њ–ґ–∞–є. –≠—В–∞ –Ј–∞–і–∞—З–∞ –љ–µ –Љ–Њ–ґ–µ—В –±—Л—В—М —А–µ—И–µ–љ–∞ –±–µ–Ј –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–≥–Њ, –≤ —З–∞—Б—В–љ–Њ—Б—В–Є, –Є–Љ–Є—В–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ –Љ–Њ–і–µ–ї–Є—А–Њ–≤–∞–љ–Є—П –Њ—В–Ї–ї–Є–Ї–∞ —Б–Є—Б—В–µ–Љ—Л вАЬ—А–∞—Б—В–µ–љ–Є–µвАЭ –љ–∞ —Г–њ—А–∞–≤–ї—П—О—Й–µ–µ –≤–Њ–Ј–і–µ–є—Б—В–≤–Є–µ вАЬ–≤–ї–∞–ґ–љ–Њ—Б—В—МвАЭ. –Ф–ї—П —Н—В–Њ–≥–Њ, –љ–∞—А—П–і—Г —Б –≤—Л—И–µ–Њ–њ–Є—Б–∞–љ–љ–Њ–є –Љ–Њ–і–µ–ї—М—О –і–ї—П –њ—А–Њ–≥–љ–Њ–Ј–Є—А–Њ–≤–∞–љ–Є—П —Г—А–Њ–ґ–∞—П –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ—Л –Љ–Њ–і–µ–ї–Є –Є –∞–ї–≥–Њ—А–Є—В–Љ—Л —А–∞–±–Њ—В [5-10].
–Ь—Л –±—Г–і–µ–Љ –Њ–њ—А–µ–і–µ–ї—П—В—М –њ—А–Њ–µ–Ї—В–љ—Г—О —Г—А–Њ–ґ–∞–є–љ–Њ—Б—В—М –њ–Њ –Љ–Њ–і–µ–ї–Є –і–ї—П —Б—А–∞–≤–љ–Є—В–µ–ї—М–љ–Њ –і–ї–Є—В–µ–ї—М–љ—Л—Е –њ—А–Њ–Љ–µ–ґ—Г—В–Ї–Њ–≤ –≤—А–µ–Љ–µ–љ–Є (—Д–∞–Ј—Л –≤–µ–≥–µ—В–∞—Ж–Є–Є):
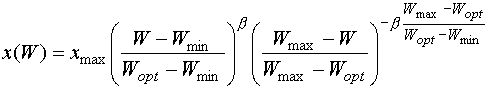 ¬†(12)
 (12)
–≥–і–µ x(W) - –њ—А–Њ–≥–љ–Њ–Ј–љ–∞—П —Г—А–Њ–ґ–∞–є–љ–Њ—Б—В—М; xmax - –Љ–∞–Ї—Б–Є–Љ–∞–ї—М–љ–∞—П —Г—А–Њ–ґ–∞–є–љ–Њ—Б—В—М —Б–µ–ї—М—Е–Њ–Ј–Ї—Г–ї—М—В—Г—А; W - –≤–ї–∞–≥–Њ–Њ–±–µ—Б–њ–µ—З–µ–љ–љ–Њ—Б—В—М –Ї–Њ—А–љ–µ–Њ–±–Є—В–∞–µ–Љ–Њ–≥–Њ —Б–ї–Њ—П –њ–Њ—З–≤—Л, –Њ–њ—А–µ–і–µ–ї—П–µ–Љ–∞—П –Ї–∞–Ї –Њ–њ–Є—Б–∞–љ–Њ –≤—Л—И–µ; Wmin, Wmax - —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ –љ–Є–ґ–љ—П—П –Є –≤–µ—А—Е–љ—П—П –≥—А–∞–љ–Є—Ж—Л –≤–ї–∞–≥–Њ–Њ–±–µ—Б–њ–µ—З–µ–љ–љ–Њ—Б—В–Є –њ–Њ—З–≤—Л, –њ—А–Є –Ї–Њ—В–Њ—А–Њ–є —Г—А–Њ–ґ–∞–є —А–∞–≤–µ–љ –љ—Г–ї—О; Wopt - –≤–ї–∞–≥–Њ–Њ–±–µ—Б–њ–µ—З–µ–љ–љ–Њ—Б—В—М, —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–∞—П xmax; - –њ–∞—А–∞–Љ–µ—В—А, —Е–∞—А–∞–Ї—В–µ—А–Є–Ј—Г—О—Й–Є–є —В–µ–Љ–њ—Л —А–Њ—Б—В–∞ —Г—А–Њ–ґ–∞—П —Б —Г–≤–µ–ї–Є—З–µ–љ–Є–µ–Љ –≤–ї–∞–≥–Њ–Њ–±–µ—Б–њ–µ—З–µ–љ–љ–Њ—Б—В–Є (–њ–∞—А–∞–Љ–µ—В—А —Б–∞–Љ–Њ—А–µ–≥—Г–ї—П—Ж–Є–Є —Б–Є—Б—В–µ–Љ—Л).
–†–µ–Ї–Њ–Љ–µ–љ–і—Г–µ–Љ —Б–Ї–∞—З–∞—В—М –і—А—Г–≥–Є–µ —А–µ—Д–µ—А–∞—В—Л –њ–Њ —В–µ–Љ–µ: –і–Є–њ–ї–Њ–Љ —Б–Є—Б—В–µ–Љ–∞, –Ї—Г—А—Б–Њ–≤–∞—П —А–∞–±–Њ—В–∞ –њ–Њ –і–Є—Б—Ж–Є–њ–ї–Є–љ–µ.
–Я—А–µ–і—Л–і—Г—Й–∞—П —Б—В—А–∞–љ–Є—Ж–∞ —А–µ—Д–µ—А–∞—В–∞ | 1 2 3 4 5 6 7 8 9 | –°–ї–µ–і—Г—О—Й–∞—П —Б—В—А–∞–љ–Є—Ж–∞ —А–µ—Д–µ—А–∞—В–∞