Предыдущая страница реферата | 1  2  3 | Следующая страница реферата

,

,

. (8)

Величины Ux , Uz и P представляют собой средние значения по ширине водохранилища соответственно Ux , Uz и P; q(x,z,t) – интенсивность боковой приточности, определяющаяся выражением:

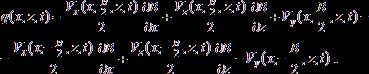 (9)

Систему (5,6) в векторной форме можно записать так:

, (10)

, (11)

где .

Считая, что движение воды безвихревое, т.е. rot  = 0, и вводя потенциал средней по ширине скорости

, (12)

из выражения (10) получаем интеграл Коши в линейном приближении:

. (13)

Компоненты средней скорости через потенциал скорости F(x, z, t) выражаются так:

,  . (14)

В связи с тем, что потенциал скорости волнового движения жидкости определяется с точностью до произвольной функции, зависящей только от времени t, произвольную функцию f(t) можно считать тождественно равной нулю. На свободной волновой поверхности должно быть задано гидродинамическое давление . При отсутствии внешнего давления .

Обозначив уравнения волновой поверхности через z = h(x, t), выражение (13) запишется так:

. (15)

Линеаризуя выражение (15), получаем:

. (16)

В линейном приближении очевидно равенство:

. (17)

Дифференцируя выражение (16) по t и подставляя в него (17), получаем:

. (18)

Из выражения (13) при f(t) = 0 для давления получается следующая его зависимость от потенциала скорости:

Рекомендуем скачать другие рефераты по теме: менеджмент, реферат условия.



Предыдущая страница реферата | 1  2  3 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки