Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10 | Следующая страница реферата



Доказательство несмещенности точечной оценки

Вывод: - нормально распределенная СВ, , , тогда чтобы найти вероятность заданного отклонения P(|a – | < d) = j

P(|a – | < d) = 2Ф() = 2Ф(), где ;    Ф() =

По таблице для функции Лапласа по значению функции равной  находим значение аргумента  ; ;      Вместо  обозначаем .;    P(|a –| < d) = P(-d< a - < d) = P(- d < a < + d) = j

(- d; + d) – доверительный интервал.

Проверка гипотез. Ошибки первого и второго рода. Мощность критерия.

В статистике рассматриваются гипотезы двух типов:

Параметрические – гипотезы о значении параметра известного распределения;

Непараметрические – гипотезы о виде распределения.

Обычно выделяют основную гипотезу – нулевую (H0). Пример: математическое ожидание признака x, который распределен по нормальному закону и дисперсия его известна, а H0: M(x) = a. Предполагаем, что известна дисперсия Конкурирующая гипотеза имеет вид: H1: M(x) ¹ a;  

H1: M(x) > a, либо H1: M(x) = a1. Для проверки гипотез используются критерии, и они представляют собой специальным образом подобранные СВ, k – точечный или приближенный закон, который известен.

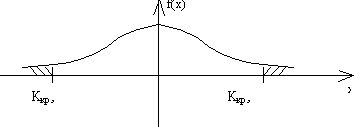
Обычно предполагается, что если гипотеза Н0 выполняется, то вычисляемая по выборочным данным kнабл. Этого критерия и гипотеза Н0 принимается, если kнабл.Î (kкритич. левостор.; kкритич. правостор.) Если kнабл. попадает в критическую область (все остальные значения k Î(- ¥ ; kкритич. лев.) È (kкритич. прав. ; ¥), то гипотеза Н0 отвергается и принимается конкурирующая гипотеза Н1. При этом возможны ошибки двух типов: Первого рода: что гипотеза Н0 отвергается, в то время, как она верна. Вероятность этой ошибки: P(H1/H0) = a - уровень значимости критерия. Критерий подбирается так, чтобы a была как можно меньше. Второго рода: что отвергается гипотеза Н1, в то время, как она верна. b = P(H0/H1) Мощностью критерия – (1-b) - вероятность попасть точке-выборке в критическое множество, когда верна конкурирующая гипотеза.

1-b = P(H1/H1)

37. Проверка гипотезы о равенстве генеральных средних при известных дисперсиях. Признак x и h распределены нормально с известными дисперсиями.

Пусть по выборкам x1, x2, ... , xn объема n, h1, h2, ... , hm объема m, получены выборочные средние значения ( ; ). Выдвигается гипотеза о равенстве генеральных средних: H0: M(x) = M(h); При конкурирующей гипотезе:

H1: M(x) ¹ M(h); В качестве проверки гипотезы выбираем новую СВ ;

- СВ:

Д(Z)- дисперсия  Д((- )/s(-)) =

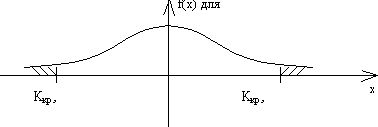
M(Z) = 0; Д(Z) = 1. Для того, чтобы выбрать Zкр. и при заданном уровне значимости a, определить принимается или не принимается основная гипотеза, найти вероятности.

P(0 < Z < Zкр.) + P(Z > Zкр. прав.) = ½ Ф(Zкр.) + a/2 = ½ Ф(Zкр. прав.) = ½ - a/2

Zнабл. =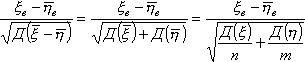

|Zнабл.| < Zкр.прав. Þ Н0  |Zнабл.| > Zкр.прав. Þ Н0 отвергается.

38. Проверка гипотезы о равенстве генеральных средних при неизвестных дисперсиях.  

Пусть x и h нормально распределенные СВ, предполагается, что неизвестны, но равны между собой дисперсии. x1, x2, ... , xn h1, h2, ... , hm

Рекомендуем скачать другие рефераты по теме: задачи курсовой работы, выборы реферат.

Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки