Предыдущая страница реферата | 1  2  3  4  5  6  7 | Следующая страница реферата

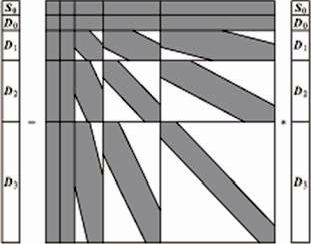Рис.1. Матричное представление при стандартном подходе к вейвлет-анализу.

 Части матрицы с ненулевыми вейвлет-коэффициентами заштрихованы.

С целью упрощения вида матричного представления было предложено использовать переопределенный набор вейвлет-коэффициентов. Сохраним эти усредненные величины в виде соответствующих промежуточных s-коэффициентов как в начальных, так и в конечных векторах, представляющих функции f и g. Конечно, в этом случае придется иметь дело с приводимыми векторами, которые намного больше требуемых для конечного ответа. Однако, известен алгоритм приведения этих переопределенных выражений к окончательной непереопределенной форме. В то же время таким образом можно существенно упростить вид матрицы преобразования и численные расчеты.

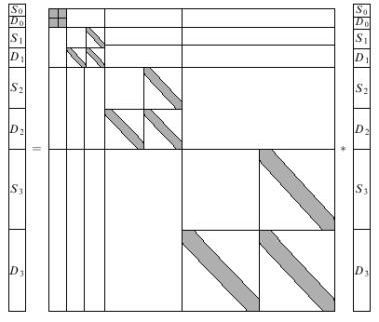
Рис.2. Нестандартное матричное умножение при вейвлет-анализе.

Различные уровни оказались полностью развязанными, потому что в матрице теперь полностью отсутствуют блоки, которые ранее перепутывали их. Блок с SS-элементами извлечен, а на его место вставлена нулевая матрица. Полная матрица соответстваенно искусственным образом увеличилась. Вместе с ней увеличились и векторы, характеризующие функции f и g. Теперь здесь удерживаются все промежуточные s-коэффициенты вейвлет-разложения функции f. Каждый блок Sj+1 получается из Sj и Dj. В матрице преобразования равны нулю все SS-элементы за исключением их величин на низшем уровне S0S0. Все остальные SD-, DS-, DD-матрицы почти диагональны вследствие конечности области задания вейвлетов и скейлинг функций. Приведенная на рис. 2 форма функции g преобразуется в ее обычное вейвлет-представление из рис. 1 путем разделения каждого Sj в Sj-1 и Dj-1 стандартным методом. Затем эти Sj-1 и Dj-1 добавляются в соответствующие компоненты вектора. Эта процедура итерируется, начиная теперь уже с Sj-1, вполоть до S0, когда мы приходим к обычному вейвлет-представлению функции g. Таким способом мы избавляемся от всех s-коэффициентов за исключением s0. Вычисления можно теперь проделать очень быстро.

4.2 Обращение матрицы

Утверждение 1. Последовательность матриц Xk такова, что

    Xk+1=2Xk -XkАXk,    (4.2.1)

    X0=aА*,    (4.2.2)

где А* - сопряженная матрица и a выбирается таким образом, чтобы наибольшее собственное значение матрицы aА*А меньше двух. Тогда последовательность сходится к обобщенной обратной матрице А-1.

Если это утверждение скомбинировать с алгоритмом быстрого матричного умножения, то получается алгоритм для построения обратной матрицы в стандартной форме с трудоемкостью  и в нестандартной форме с трудоемкостью , где R – число обусловленности матрицы. С помощью числа R можно оценить соотношение между наибольшим и наименьшим сингулярными числами выше порога точности.

4.3 Вычисление экспоненты, синуса и косинуса от матрицы.

При обращения матрицы использовался ранее известный алгоритм, который выходит на совершенно иной уровень, когда применяется вместе с вейвлет-представлением.

Алгоритм вычисления экспоненты матрицы основывается на тождестве

   .    (4.3.1)

Во-первых, exp(2-LA) может быть посчитана, например, с помощью ряда Тейлора. Число L выбирается таким образом, чтобы наибольшее сингулярное число матрицы 2-LA было меньше единицы. На втором шаге алгоритма для достижения результата матрица 2-LA возводится в квадрат L раз.

Аналогично, синус и косинус от матрицы могут быть посчитаны с исподьзованием формул двойного угла.

        (4.3.2)

    ,    (4.3.3)

при l=0,…,L-1

        (4.3.4)

    ,    (4.3.5)

где I – тождество. Снова выбираем L таким образом, чтобы наибольшее сингулярное число матрицы 2-LA было меньше единицы, вычисляем синус и косинус матрицы 2-LA, с помощью рядов Тейлора, а затем используем формулы (4.3.4) и (4.3.5).

Обычно такие алгоритмы требуют по меньшей мере O(N3) операций, так как должне быть выполнено достаточно много операций по умножению густых матриц. Быстрый алгоритм для умножения матриц в стандартной форме уменьшает сложность до не более чем  операций, а быстрый алгоритм для умножения матриц в нестандартной форме – до O(N) операций.

Рекомендуем скачать другие рефераты по теме: доклады 7 класс, конспект.



Предыдущая страница реферата | 1  2  3  4  5  6  7 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки