Рефераты | Рефераты по математике | Матроид Матроид Категория реферата: Рефераты по математике Теги реферата: рефераты бесплатно скачать, наука реферат Добавил(а) на сайт: Амалиев. Предыдущая страница реферата | 1  2  3 | Следующая страница реферата

3. Если A, B ∈ I, причем |A| = |B| + 1, тогда существует элемент x ∈ B − A, такой что B ∪ {x} ∈ I.

Докажем, что в рассмотренном примере множество линейно независимых столбцов действительно является матроидом. Для этого достаточно доказать третье свойство из определения матроида. Проведем доказательство методом от противного.

Доказательство. Пусть  и . Пусть W будет пространством векторов, охватываемым . Понятно, что его размерность будет не менее . Предположим, что  будет линейно зависимо для всех  (то есть третье свойство не будет выполняться). Тогда B образует базис в пространстве W. Из этого следует, что .Но так как по условию A и B состоят из линейно независимых векторов и , получаем противоречие. Такое множество векторов будет являться матроидом.

Дополнительные понятия

Двойственным данному матроиду называется матроид, носитель которого совпадает с носителем данного матроида, а базы — дополнения баз данного матроида до носителя. То есть X*=X, а множество баз двойственного матроида — это множество таких B*, что B*=XB, где B — база данного матроида.

Циклом в матроиде называется такое множество A⊂X, что A∉I, и для любого B⊂A, если B≠A, то B∈I

Рангом матроида называется мощность его баз. Ранг тривиального матроида равен нулю.

Матроид Фано

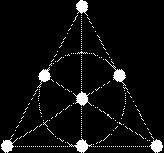Матроиды с маленьким числом элементов часто изображают в виде диаграмм. Точки — это элементы основного множества, а кривые «протянуты» через каждую 3-ех елементную цепь (3-element circuit). Диаграмма показывает 3-ранговый матроид, называемый матроидом Фано, пример, который появился в 1935 в статье Уитни (Whitney).

Название возникло из того факта, что матроид Фано представляет собой проективную плоскость второго порядка, известная как плоскость Фано, чьё координатное поле — это двух-элементное поле. Это означает, что матроид Фано — это векторный матроид, связанный с семью ненулевыми векторами в трехмерном векторном пространстве над полем 2ух элементов.

Из проективной геометрии известно, что матроид Фано непредставим произвольным множеством векторов в вещественном или комплексном векторном пространстве (или в любом векторном пространстве над полем, чьи характеристики отличаются от 2).

Графовый матроид

Граф неориентированный и состоит из четырех вершин и семи ребер, одно из которых является петлей. Пусть E будет множеством, состоящих из ребер этого графа,, а I будет множеством подмножеств E, таких что каждый элемент I не содержит в себе циклов графа. Эта пара множеств E, I является матроидом, ее называют графовым матроидом и обозначают M(G).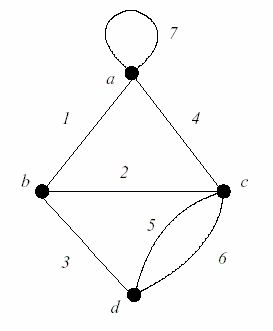

Теорема

Пусть G — граф, а — его матрица инциденций. Если рассматривать  как матрицу над полем {0,1}, где все операции выполняются по модулю 2, то тогда векторный матроид, построенный на , в качестве независимых множеств будет содержать множества ребер, не содержащих в себе циклов, и .

Доказательство. Необходимо доказать, что  линейно зависим тогда и только тогда, когда X содержит цикл. Предположим, что X содержит в себе цикл C. Если C — это петля, то тогда в X будет содержаться нулевой вектор и он будет линейно зависимым. Если же C не петля, то каждая вершина в этом цикле будет соответствовать двум ребрам C и сумма векторов по модулю 2 будет нулевым вектором. Из-за чего X будет линейно зависимым.

Теперь предположим, что X линейно зависимый. Возьмем минимальное линейно зависимое подмножество D из X (то есть такое подмножество, что удаление из него любого элемента приводит к тому, что оно будет линейно независимым). Если D будет состоять из нулевого вектора, то тогда X содержит петлю и, соответственно, цикл.

Если D не содержит нулевого вектора: так как в поле {0,1} существует единственный ненулевой элемент — 1, то сумма векторов из D будет нулевым вектором, из-за того, что D — минимальное линейно зависимое подмножество. Из этого следует, что D содержит ребра из цикла, и если какой-то вершине инцидентно ребро из D, то существует как минимум еще одно ребро, инцидентное ей. Действительно, возьмем ребро  и пусть вершины  и соответствуют этому ребру. Пусть вершине инцидентно еще какое-то ребро . Пусть вершина  будет другим концом ребра . Продолжим этот процесс. В результате будут получены две последовательности —  и . Так как количество вершин в D конечно, то какая-то из вершин v должна повториться. Когда это произойдет, то в D будет найден цикл. Соответственно цикл будет найден и в X.

Матроиды и комбинаторная оптимизация

Матроиды имеют широкое применение в задачах, связанных с комбинаторной оптимизацией, а также с задачами, решение которых основано на жадных алгоритмах.

Рассмотрим такую задачу: у менеджера есть m однодневных работ для одного человека . Также он располагает n рабочими, каждый из которых умеет выполнять какой-то поднабор работ. Менеджер хочет знать, какое максимальное количество работ способны выполнить его рабочие за один день. Как позже выяснится, это будет рангом некоего матроида.

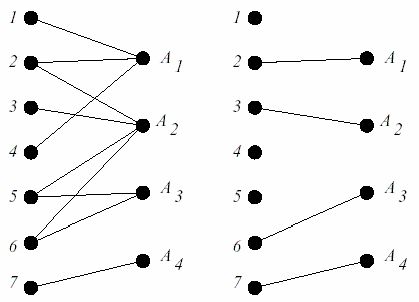
Пусть A — множество подмножеств некоего множества E. К примеру, пусть A=({1,2,4},{2,3,5,6},{5,6},{7}), при множестве E={1,2,3,4,5,6,7}. Подмножество E —  называется частичным трансверсалем A, если есть взаимооднозначное соответствие Ф между {1,2,…,k} и {1,2,…,m}, причем  для любых i. Если m = k, то такой частичный трансверсаль называется трансверсалем. Если взять множество {2,3,6,7}, то оно будет трансверсалем для A, как это видно из рисунка слева.

Теоремы

Все базы матроида имеют одинаковую мощность.

Рекомендуем скачать другие рефераты по теме: bestreferat, quality assurance design patterns системный анализ.



Предыдущая страница реферата | 1  2  3 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки