Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

 (1.17)

где  и  – плотности s-электронов n-й оболочки со спином, параллельным и антипараллельным магнитному моменту атома.

В чистом ферромагнитном железе наряду с поляризацией оболочек внутренних и внешних s-электронов существуют другие источники магнитного поля на ядре. Вклад в магнитное поле даёт орбитальный момент электронов. Согласно данным [7.12], в металлическом железе напряженность магнитного поля, создаваемая незамороженным орбитальным моментом 3d-электронов, равна ~ + 70 кЭ. Другим источником поля является вклад от магнитных моментов соседних атомов, рассматриваемых как магнитные диполи. Для кубических кристаллов, состоящих из одинаковых атомов, этот вклад равен нулю. В железе и его сплавах напряженность эффективного магнитного поля определяется степенью поляризации электронов проводимости с 3d-электронами атома железа.

Как следует из соотношения (1.16), величина магнитного расщепления ядерных уровней и, соответственно, расстояние между линиями секстета определяются произведением постоянного ядерного μ и переменного атомного H сомножителей. Это позволяет измерять поля на ядрах атомов магнитных материалов, изучать механизмы их формирования, а также исследовать влияние на эффективное магнитное поле на ядре таких факторов, как состав, температура, давление, наложение внешних полей и т.д.

Теоретическая форма мессбауэровского спектра при наличии магнитного расщепления ядерных уровней может быть представлена суперпозицией лоренцевских линий:

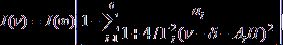, (1.18)

где  – коэффициенты, учитывающие тонкую структуру энергетических уровней ядра Fe и задаваемые матрицей (0,5; + 0,289; + 0,079; - 0,079; - 0,289; - 0,5).

Следует заметить, что в магнитоупорядоченных сплавах зачастую наблюдается комбинированное (магнитное и электрическое) сверхтонкое взаимодействие. Общего решения такой задачи (расчета положения энергетических уровней ядра) не существует. Для случая аксиально симметричного тензора градиента электрического поля сверхтонкая структура ядерных уровней и вид мессбауэровского спектра при комбинированном взаимодействии показаны на рис. 1.3.г. Во многих практически важных случаях, например, для обладающих кубической симметрией твердых растворов замещения, сдвиги линий спектра за счет квадрупольного расщепления (вследствие локальных искажений кубической симметрии, обусловленных различием эффективного заряда и радиуса компонентов) очень малы и или в первом приближении можно пренебречь.

1.4. ШИРИНА РЕЗОНАНСНОЙ ЛИНИИ.

Ширина резонансной линии в идеальном случае тонкого поглотителя (см. (1.5)) равна удвоенной естественной ширине (Г = ћ/τ, τ – среднее время жизни ядра в возбуждённом состоянии). В реальном эксперименте имеет место аппаратурное уширение линии, определяемое характеристиками данного конкретного мессбауэровского спектрометра (уровнем вибраций, линейностью, стабильностью и т.д.), уширение, обусловленное самопоглощением в источнике и поглотителе вследствие их конечной толщины [6], и, наконец, уширение, связанное с относящимися к предмету изучения физическими причинами. К последним относятся динамические эффекты, обусловленные движением атомов [13], а также эффекты, связанные с наличием широкого спектра состояний мессбауэровских ядер в кристалле вследствие вариаций их локального атомного и электрического окружения (при этом уширенная резонансная кривая представляет собой суперпозицию близко расположенных смещенных друг относительно друга или частично расщепленных линий). Уширение мессбауэровской линии может быть вызвано высокой плотностью точечных дефектов и дислокаций [16].

1.5. О СТРУКТУРЕ КРИВЫХ РЕЗОНАНСНОГО ПОГЛОЩЕНИЯ НЕИДЕАЛЬНЫХ КРИСТАЛЛОВ.

Соотношения (1.10), (1.15), (1.18) описывают форму мессбауэровских спектров кристаллов, все атомы которых имеют идентичное кристаллографическое, химическое и, соответственно, электрическое и магнитное состояния. Однако даже в строго упорядоченных кристаллах и химических соединениях атомы одного и того же элемента могут находиться в различных структурных позициях, иметь разную валентность и строение внешних электронных оболочек.

Число различных состояний атомов резко возрастает для нестехиометрических, а также стехиометрических, но частично разупорядоченных фаз. Большим числом неидентичных состояний атомов характеризуются неупорядоченные твердые растворы, каковыми зачастую являются сплавы металлов. Резонансные атомы в таких системах могут находиться во множестве неэквивалентных позиций.

В реальных сплавах может наблюдаться целый спектр неодинаковых состояний резонансных атомов (и их ядер) в силу различия конфигураций ближайшего окружения этих атомов химическими элементами и дефектами в радиусе нескольких ближайших координационных сфер. Наличие высокой плотности точечных дефектов, ядер дислокаций, межфазных границ, границ зерен может вызвать изменение состояния значительного числа атомов.

Неодинаковыми являются и состояния мессбауэровских ядер в различных фазах сплава.

В силу различных параметров сверхтонкого взаимодействия для резонансных атомов, находящихся в различных неэквивалентных положениях в решетке, мессбауэровские спектры реальных кристаллов часто представляют собой весьма сложную суперпозицию откликов от большего числа индивидуально поглощающих резонансных ядер.

В связи с этим экспериментальные спектры содержат исключительно важную (зачастую уникальную) информацию о топографии и динамике атомов кристалла. Получить указанную информацию можно лишь в том случае, если известна взаимосвязь между параметрами мессбауэровского спектра и параметрами твердого тела, т.е., фактически, когда записана форма кривой резонансного поглощения как функция параметров, относящихся к атомной, электронной структуре и динамике атомов кристалла.

Анализируя соотношения, представленные в § 1.2, можно заключить, что параметры, относящиеся к динамике атомов, и параметры, задающие число резонансных ядер в различных неэквивалентных состояниях в кристалле, определяют амплитуду лоренцианов. Число же неэквивалентных состояний определяет число субспектров в составе мессбауэровского спектра, а параметры сверхтонких – положение линий субспектров на шкале энергий.

В качестве примера на рис. 1.4 приведены мессбауэровские спектры чистого железа (а) и закаленного от 820 °C сплава железа

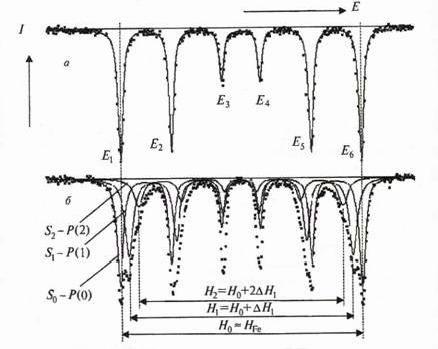
Рис. 1.4. Мессбауэровские спектры чистого железа (а) и твердого раствора Fe + 8,25 ат. % Mn (б) ( = 300 °C); , ,  – площади, ограниченные тремя наиболее интенсивными секстетами линий спектре поглощения (P (0), P (1), P (2) – вероятности окружения атома железа l¹ = 0, 1, 2 ближайшими атомами Mn); ∆ от атома Mn в 1-й координационной сфере Fe (

с 8,25 ат. % Mn (б) с хаотическим распределением атомов Fe и Mn по узлам кристаллической решетки. На рисунке представлено разложение спектра сплава на три зеемановских секстета линий, подобных спектру чистого железа, но отличающихся значениями эффективного манитного поля.

Как следует из классических работ М. Стирнс, Г. Вертхейма и их коллег, секстет линий с максимальным значением поля  отвечает атомам железа, в первой координационной сфере которых нет атомов примеси (в данном случае Mn). Секстеты  и  соответствуют атомам Fe, у которых среди ближайших соседей есть, соответственно, 1 и 2 атома Mn.

Для разбавленных сплавов выполняется правило аддитивности вкладов, а именно:  и  (в общем случае , где  – вклад в эффективное магнитное поле от атома марганца на первой координационной сфере). Интенсивности трех рассматриваемых секстетов линий пропорциональны вероятностям P(l) окружения атома Fe различным числом l=0, 1, 2, …z атомов примеси (z – координационное число для 1-й координационной сферы в ОЦК решетке). Аналогичное влияние атомов примеси наблюдается и для изомерного сдвига: , ,  и т.д., где  – вклад в изомерный сдвиг от атомов примеси 1-й координационной сферы. Значения  (где i – номер координационной сферы), выраженные в значениях доплеровской скорости, очень малы. Соответственно мал и визуальный наблюдаемый сдвиг компонент спектра (в данном случае секстетов линий). Математическая обработка спектров позволяет определить значения  и  и оценить их погрешности.

В неупорядоченном сплаве вероятности P(l) определяются биномиальным распределением:

Рекомендуем скачать другие рефераты по теме: правила реферата, bestreferat.



Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки