Нахождение неопределенных интегралов
Категория реферата: Рефераты по математике
Теги реферата: мировая торговля, реферат революция
Добавил(а) на сайт: Гуковский.
Предыдущая страница реферата | 1 2 3 4
Рефераты | Рефераты по математике | Нахождение неопределенных интегралов
Категория реферата: Рефераты по математике Теги реферата: мировая торговля, реферат революция Добавил(а) на сайт: Гуковский. Предыдущая страница реферата | 1 2 3 4 |
68,85 |
215,78 |
Составим для определения коэффициентов систему уравнений вида:
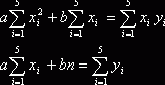
Получим
Решая систему методом исключения определяем:
Искомая эмпирическая формула y=28.23-4.45x
Значение переменной при x=4.0
y=28.23-4.45*4=10.43
7. Исследовать сходимость ряда.
Исследуем ряд сначала на абсолютную сходимость. Общий член ряда
В свою очередь
ряд 
расходится как
гармонический. Значит абсолютной сходимости у исходного ряда нет. Исследуем на
условную сходимость по признаку Лейбница.
при 
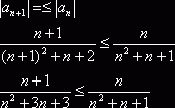
действительно
для 
По признаку Лейбница, исходный ряд сходится условно.
Скачали данный реферат: Матильда, Маринкин, Лозанов, Tekusa, Злата, Аносов.
Последние просмотренные рефераты на тему: правовые рефераты, реферат электрические, доклады 7 класс, скачати реферат на тему.
Предыдущая страница реферата | 1 2 3 4