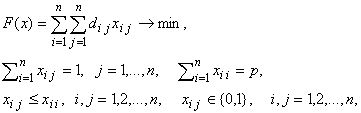Некоторые свойства многогранника. Задачи о P-медиане

Г.Г. Забудский, Институт информационных технологий и прикладной математики СО РАН

1.  Постановка задачи и определения

Задачи оптимального размещения объектов имеют много практических приложений. Описываются различные постановки таких задач [1-8]. В данной статье рассматривается известная NP-трудная задача оптимального размещения на графе - задача о p-медиане [1,7-8]. Для ее исследования здесь применяется подход, развиваемый в работах А.А. Колоколова и других [2,4-7,9] для анализа и решения задач целочисленного программирования, основанный на разбиении допустимой области соответствующей непрерывной задачи. В данной работе рассматривается L- разбиение.

Задача о p-медиане сводится к простейшей задаче размещения (ПЗР). Сводимость не гарантирует сохранения некоторых свойств. Например, многогранник ПЗР - квазицелочисленный, а многогранник задачи о p- медиане в общем случае является только связноцелочисленным (квазицелочисленным при p = 1, n-1, где n - число вершин графа) [1].

В работе [2] доказано, что многогранник ПЗР имеет альтернирующую L-структуру. В данной статье показано, что многогранник задачи о p-медиане также имеет альтернирующую L -структуру.

Рассматривается целочисленная модель задачи о p- медиане:

где n - количество вершин графа; dij - кратчайшее расстояние между i-й и j- й вершинами графа; p- количество размещаемых объектов. Диагональными будем называть элементы вектора x = (x11,x12,...,xnn) с одинаковыми индексами, а медианными - диагональные, принимающие значение 1. Переменная xij = 1, если вершина j"прикреплена" к вершине i. Условия (4) гарантируют прикрепление только к медианным вершинам. Если условия (5) заменить линейными неравенствами

то ограничения (2)-(4),(6) задают многогранник в пространстве размерности n2. Обозначим его через Mp.

Введем определение L-разбиения . Пусть Zk- множество всех k-мерных целочисленных векторов. Тогда L-разбиение непустого множества Rk определим следующим образом:

1) каждая точка zZk образует отдельный класс;

2) нецелочисленные точки x и y эквивалентны, если (x) = (y) и [xi=yi, i =1,...,(x)-1, [x(x)] = [x(x)] , где(x) - номер первой дробной, [a] - наибольшее целое число, не превосходящее a.

В выпуклых множествах с альтернирующим L-разбиением дробныеи целочисленные классы чередуются. В работе [9] предложен критерий альтернируемости L-разбиения:выпуклое замкнутое множество Rk имеет альтернирующее разбиение тогда и только тогда, когда для любого дробного L-класса V существуют целочисленные точки z1,z2    Zk ( называемые окаймляющими) такие, что для любого x  V  z1j = z2j = xj,  j =1,...,(x)-1; z2j = [xj];    j = (x); z1j = ]xj[;   j = (x),

где ]a[ - верхняя целая часть числа a. Ясно, что знак лексикографического сравнения.

2.  Структура L-разбиения

Исследуем структуру L-разбиения многогранника Mp.

ТЕОРЕМА. Для произвольного упорядочения переменных многогранник Mp имеет альтернирующую L-структуру .

Доказательство. Воспользуемся критерием альтернируемости L-структуры. Возьмем произвольный дробный xMp. Обозначим через  произвольную перестановку n2 индексов вектора x, т.е. пар чисел от 1 до n. Тогда (i,j) - номер пары (i,j) в перестановке  .Рассмотрим два случая.

1. Пусть первая дробная в векторе x  Mp - диагональная, т.е. (x) = (i,i) и  Отметим, что qZ, qp, а тогда q+1 p. Построим вектор z1  Mp Zn2, и . Возможны варианты.

1.1. q+1 = p. Для каждого j такого, что найдется kj такой, что 0xkj1 построим множество Jj =xkk = 1. Покажем, что Jj.

Действительно, пусть нашелся j, для которого  Jj=, тогда 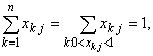а так как xkjxkk для любых k и j, имеем а из условия получаем 0 xij1 и тогда iJj, что противоречит тому, что Jj=.

Вектор z1 строим следующим образом: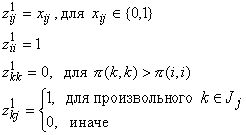

Нетрудно проверить, что .

Поделитесь этой записью или добавьте в закладки