Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Естественно, рассмотрение материала должно начинаться с определения основного понятия — понятия расплывчатого (нечеткого) множества.

Пусть Х = {х} — совокупность объектов, обозначенных через х. Расплывчатое множество А в X есть совокупность упорядоченных пар А = {х, µа (х)}, х Є X, µа (х) — степень принадлежности х множеству А, то есть µа (х) — это функция, ставящая каждому элементу х из X в соответствие какое-то (одно) число из отрезка [0; 1].

Обычное множество — это множество, для которого ц равно либо нулю, либо единице, скажем, множество четных чисел. Примером нечеткого множества может быть множество А «несколько чисел» для множества X = {0; 1; 2;...} всех неотрицательных чисел.

А = {(1; 0,0), (2; 0,05), (3; 0,2), (4; 0,6), (5; 0,8), (6; 1,0), (7; 1,0), (8; 0,8), (9; 0,6), (10; 0,2), (11; 0,05), (12; 0,0)}.

В данном примере утверждается, что одно число еще не может, а 12 чисел уже могут попадать в множество «нескольких чисел», два числа и одиннадцать чисел лишь при очень большом желании, образно говоря, могут быть охарактеризованы как несколько чисел, 6 или 7 чисел признаются таким количеством чисел, которые в данном контексте, бесспорно, отнесены автором примера к числу объектов, обладающих определенным свойством, и т. д.

Рассмотрим еще один пример, иллюстрирующий, как используются нечеткие множества. Пусть примерно прямая линия АБ — это любая линия, проходящая через точки А и Б так, что расстояние d, от каждой точки АБ до («истинной») прямой (АБ)° по отношению к длине (АБ)° мало, d — нечеткая переменная (читатель может сам определить d). Примерно средней точкой М на АБ назовем такую точку, расстояние от которой до М° — середины (АБ)° — мало.

С использованием приведенных понятий можно для известной теоремы о трех медианах треугольника (три медианы треугольника пересекаются в одной точке) сформулировать аналог — нечеткую теорему. Пусть АВС — примерно равносторонний треугольник с вершинами А, В, С, а М1, М2, М3 — примерно середины сторон ВС, АС, АВ.

Тогда примерно прямые АМ1, ВМ2, СМз образуют «примерно» треугольник Т1Т2T3, который более или менее мал в сравнении с треугольником АВС (рис. 2.2).

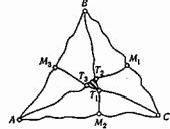
Рис. 2.2. Нечеткая теорема о трех «медианах»

Конечно, приведенные примеры скорее забавны, чем практически полезны, но дело в том, что мы постоянно пользуемся нечеткими понятиями, рассуждениями, множествами, теоремами:

• у корпорации X прекрасные перспективы;

• на фондовой бирже наблюдается резкий спад;

• корпорация У использует прогрессивную технологию и т. д.

Обратите внимание на то, что для описания расплывчатости недостаточно теории вероятностей и статистических методов, они предназначены для работы со случайностью, когда речь идет о принадлежности некоторого объекта к четкому множеству. Скажем, последний из приведенных примеров содержит расплывчатое утверждение вследствие неточности, нечеткости выражения «прогрессивная технология», в то время как утверждение «вероятность того, что фирма 2 работает в убыток, равна 0,8» содержит информацию о мере неопределенности относительно принадлежности 2 к четкому множеству фирм, работающих в убыток.

Люди, в отличие от ЭВМ, обладают способностями оперировать расплывчатыми понятиями и выполнять расплывчатые инструкции (вспомните русскую народную сказку, в которой герой блестяще выполнил одну из таких инструкций: «Пойди туда, не знаю куда, принеси то, не знаю что»). Люди также способны на интуитивном уровне оперировать с расплывчатыми целями («Фирме надо сохранить за собой около 15—20% рынка»), расплывчатыми ограничениями («Фирма не может потратить на рекламу значительную часть квартального дохода») и с расплывчатыми решениями («На рекламу будет выделено около 5—8% дохода»).

При том подходе к принятию решений в расплывчатых условиях, который развит Р. Беллманом и Л. Заде, и цель, и ограничения рассматриваются как расплывчатые множества в пространстве альтернатив.

Если X = {х} — заданное множество альтернатив, то расплывчатая цель Q отождествляется с фиксированным расплывчатым множеством Q в X. Например, если X — действительная прямая, а расплывчатая цель формулируется как «х должно быть значительно больше 10» (скажем, доход должен быть таким в каких-то известных единицах), то эту цель можно представить как расплывчатое множество с функцией принадлежности

Расплывчатое ограничение С в пространстве X определяется таким же образом, то есть как некоторое расплывчатое множество в X. Если, как и для цели, X — действительная прямая, то ограничение «х должно быть приблизительно в окрестности 15» (такими могут быть ограничения на затраты) представимо с помощью функции принадлежности

Если в пространстве альтернатив X заданы расплывчатая цель Q и расплывчатое ограничение С, то расплывчатое множество D, образованное пересечением Q и С, называется расплывчатым решением. В специальных работах показано, что для D = Q П С,

будет

В условиях приводимых выше примеров

Рекомендуем скачать другие рефераты по теме: мировая экономика, доклад по обществознанию.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки