Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

– О чём вы думаете? – спросил его Гельфанд, с трудом поднимаясь с земли. – Не о том ли, что Гаусс и Зейдель придут не туда, куда направлялись?

– Вы угадали. Они собирались найти самую низкую точку, представляя себе местность в виде впадины с гладкими стенками (рис. 2). Но судьба может сыграть с ними злую шутку: им может встретиться на пути овраг. И он быстро начертил на листке из судового журнала рисунок 3.

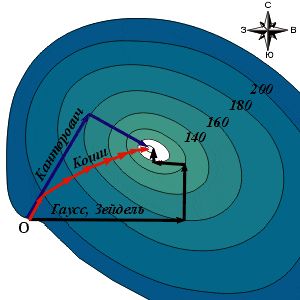
Рис. 2

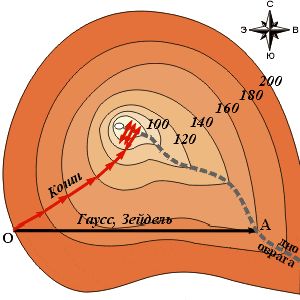
Рис. 3

– Их счастье, если по дну оврага протекает ручей. А если родник в самой низкой точке?

– Да, тогда судьбе Гаусса и Зейделя не позавидуешь: идя на восток, они придут в точку A – это самое низкое место на их пути. А в направлении север-юг самая низкая точка – это снова точка A. Таким образом, бедняги придут к выводу, что A – самая низкая точка на местности и умрут в ней от жажды.

– Но может быть, их спасёт фляжка Коши?

– Боюсь, что и фляга Коши останется пустой, если он встретится с оврагом. Оказавшись у дна оврага, он будет искать направление самого крутого спуска, и оно неизбежно приведёт его в точку по другую сторону оврага. Из этой точки он вернётся на прежнюю сторону и дальше пойдёт небольшими шажками до тех пор, пока жажда не свалит его. Ведь весь овраг он увидеть не может – его фонарь способен осветить местность лишь у самых ног. Надо придумать что-нибудь другое...

– А что если Канторович достигнет цели? Хотя не думаю: если овраг искривлён, а овраги редко бывают прямыми, то он начнёт метаться по дну оврага, почти не приближаясь к цели. Надо стараться двигаться по дну оврага.

– Разумеется, но как? Впрочем... кажется, придумал. Посмотрите на рисунок 4. Давайте мы оба, вы и я, пойдём из двух разных точек методом Канторовича. Скажем, я отсюда, а вы – отойдя шагов на сто в любом направлении.

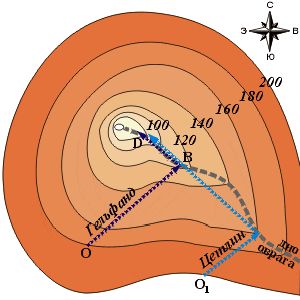
Рис. 4

– Понятно, а дальше? Ага, дальше мы оба спустимся на дно оврага и постараемся увидеть фонари друг друга. Допустим, нам это удастся. Тот из нас, чей фонарь выше, двинется по направлению к тому, чей фонарь ниже.

– Но встретившись, не остановится, а пройдет дальше в том же направлении до точки D. Из этой точки он снова спустится на дно оврага, и мы опять попытаемся увидеть друг друга. И так до тех пор, пока уровень на дне оврага не укажет горизонтальный участок.

И, выбрав фонари поприметнее, оба отправились каждый своим путём.

– А вы, я вижу, не торопитесь к влаге? – спросил Растригина Винер. – Иначе почему бы вам не воспользоваться одним из весьма разумных способов, которые предложили наши друзья по несчастью?

– У всех этих способов один недостаток – слишком много приходится возиться с уровнем, пока найдёшь нужное направление. А что если пойти по какому-либо направлению наугад, пока оно ведёт на спуск? Потом изменить направление и снова спускаться по нему. Изменить, разумеется, тоже наугад. Разве таким образом я не приду к цели? Стоит ли терять время на отыскание направления наискорейшего спуска, если уже через несколько шагов оно перестает им быть?

И не успел Винер возразить или согласиться, как Растригин закрыл глаза, повернулся несколько раз на месте, как делают при игре в жмурки, и отправился в темноту.

Методы спуска

Необходимость найти максимум или минимум (объединяемых названием «экстремум» – «крайнее значение») некоторой функции возникает во многих задачах экономики и техники. А местность можно считать макетом функции двух переменных, скажем широты и долготы. Значение функции – это высота местности (над уровнем моря) в данной точке, горизонтали – линии уровня, вдоль них функция постоянна. И ситуация, возникающая при поиске экстремума, во многом сходна с той, в которой оказались неудачливые путешественники. Поиск экстремума происходит как бы в темноте, единственным средством ориентации служат значения минимизируемой (максимизируемой) функции в какой-то точке, а также направления её наискорейшего убывания или возрастания.

Придумано уже немало методов отыскания экстремума. Не случайно, как заметил читатель, фамилии потерпевших кораблекрушение совпадают с фамилиями ряда математиков прошлого и настоящего, которые решали эту проблему. А путь, которым они отправились, показывает сущность их методов отыскания экстремума.

Великий француз П.Ферма (1601–1665) первым ясно осознал и сумел описать аналитически свойство экстремума гладкой непрерывной функции: касательная в этом месте должна быть горизонтальна. К.Гаусс (1777–1855) и А.Зейдель (1821–1896), следуя своему методу покоординатного спуска, по очереди спускались то вдоль одной, то вдоль другой координаты. Спускались до тех пор, пока касательная к направлению движения не станет горизонтальной. А положение уровня естественно определяет направление касательной.

Обратите внимание на то, что Гаусс и Зейдель не стремились спускаться по тому направлению, где крутизна больше всего. К этой идее первым пришёл О.Коши (1789–1857). Вектор, указывающий направление (вверх) с наибольшей крутизной, называется градиентом, а сам метод Коши – градиентным методом. Именно по градиенту стал бы прокладывать свой путь Коши, если бы его целью была самая высокая точка местности, чтобы осмотреться. Но вспомним, что на острове стояла мгла кромешная и целью Коши была вода. Поэтому он отправился по направлению наискорейшего убывания высоты местности, или по направлению антиградиента. Для определения антиградиента функции существуют точные и приближённые методы, но нам достаточно представить себе уровень, который мы прикладываем к земле и разыскиваем то направление, при котором воздушный пузырёк быстрее всего убегает к краю шкалы. Конечно, способ этот весьма неточен, да и мороки с ним немало. Но и для определения градиента с помощью упомянутых аналитических методов тоже приходится повозиться.

Рекомендуем скачать другие рефераты по теме: пример курсовой работы, реферат на тему предприятие.



Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки