Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

В общем случае вейвлет преобразование функции f(t) выглядит так:

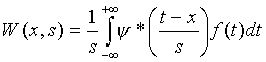(2)

где t – ось времени, x – момент времени, s – параметр, обратный частоте, a (*) – означает комплексно-сопряженное.

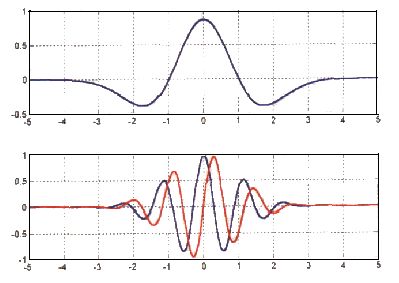
Рис 1. Примеры вейвлетов.

Главным элементом в вейвлет анализе является функция-вейвлет. Вообще говоря, вейвлетом является любая функция, отвечающая двум вышеуказанным условиям. Наибольшей популярностью пользуются два изображенных на рисунке 1 вейвлета:

Сверху изображен вейвлет “сомбреро” (Mexican Hat), названный так благодаря своему внешнему виду. На нижней части рисунка 1 изображен вейвлет Морле. График любого вейвлета выглядит примерно также, как и вейвлет Морле. Заметим, что вейвлет Морле – комплекснозначный, на рисунке изображены его вещественная и мнимая составляющие.

Итак, у нас имеется некоторая функция f(t), зависящая от времени. Результатом ее вейвлет-анализа будет некоторая функция W(x,s), которая зависит уже от двух переменных: от времени и от частоты (обратно пропорционально). Для каждой пары x и s рецепт вычисления вейвлет преобразования следующий:

Функция вейвлет растягивается в s раз по горизонтали и в 1/s раз по вертикали. Далее он сдвигается в точку x. Полученный вейвлет обозначается ψ(x,s). Производится усреднение в окрестности точки s при помощи ψ(x,s).

В результате “вырисовывается” вполне наглядная картина, иллюстрирующая частотно-временные характеристики сигнала. По оси абсцисс откладывается время, по оси ординат – частота (иногда размерность оси ординат выбирается так: log(1/s), где s-частота), а абсолютное значение вейвлет преобразования для конкретной пары x и s определяет цвет, которым данный результат будет отображен (чем в большей степени та или иная частота присутствует в сигнале в конкретный момент времени, тем темнее будет оттенок).

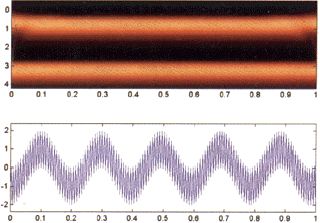
Рис 2. Вейвлет преобразование стационарного сигнала.

Данный рисунок показывает результаты вейвлет анализа для сигнала, представляющим из себя наложение двух синусоид различной частоты. Частотные характеристики данного сигнала не меняются во времени (сигнал стационарный), что хорошо видно на верхней части рисунка 2.

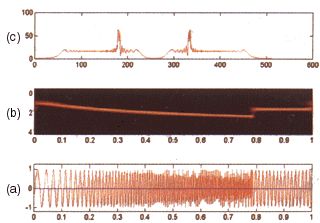
Рис 3. Сравнение методов анализа.

По рисунку 3 удобно сравнить результаты, которые дают преобразование Фурье и вейвлет преобразование. Исходный сигнал изображен на рис (3a). Как видно из рис (3c) преобразование Фурье дает информацию о том спектре частот, который присутствует в сигнале в промежутке времени от 0 до 1 сек., при этом нам неизвестно когда именно та или иная частота реально присутствовала в сигнале.

В то же время вейвлет преобразование (3b) дает исчерпывающую картину динамики изменения частотных характеристик во времени. Все это указывает на то, что вейвлет преобразование существенно более информативно по сравнению с преобразованием Фурье.

3.3.1 Методы вычисления непрерывного вейвлет-преобразования.

Существует два разных пути проведения вейвлет преобразования. Речь идет о расчетах во временной и частотной областях. При работе во временной области мы имеем дело с функциями, аргументами которых являются временные параметры, а в случае частотной – частотные. В частотной области используется механизм быстрого преобразования Фурье. [5c]

3.3.1.1 Во временной области

Прежде всего, нам необходимо определить материнский вейвлет. Допустим, мы выбрали некоторую функцию, удовлетворяющую необходимым условиям: ψ0(η), где η – безразмерный период.

Итак, нам дана временная серия X, со значениями xn, в моменты времени nÎ [0,N-1], где N – количество измерений. Каждая величина разделена по времени на постоянную величину dt. Получив основную формулу для материнского вейвлета, необходимо иметь возможность изменять размеры вейвлета. Для этого строится так называемый "масштабированный" вейвлет который будет иметь вид:

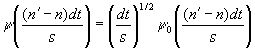(3)

s – параметр, обратный частоте.

Вычисление вейвлет преобразования является сверткой искомой временной серии с функцией-вейвлетом. Основная формула имеет вид :

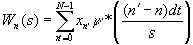(4)

в данном случае (*) – означает комплексно-сопряженное.

Результатом расчета Wn(s) по формуле (4) будет комплексное число. В качестве конечного результата берется абсолютное значение полученного комплексного числа. [5a]

Блок – схема алгоритма:

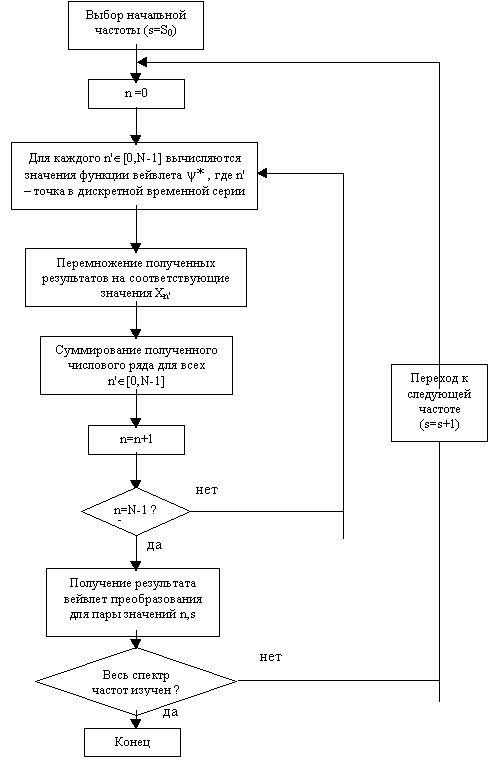
3.3.1.2 В частотной области

Вейвлет преобразование можно провести в частотной области. Для этого снова в первую очередь необходимо определить материнский вейвлет. Расчет по данной схеме происходит следующим образом: преобразование Фурье самого вейвлета (в данном случае будем рассматривать вейвлет Морле) сконцентрировано вокруг некоторой выделенной частоты w 0 ≠ 0. Поэтому преобразование Фурье вейвлета, растянутого в s раз, будет сконцентрировано вокруг частоты w 0/s (см рис. 4).

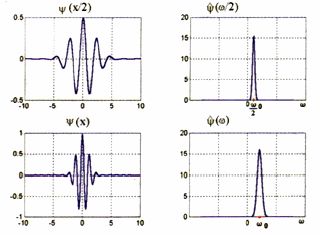
Рис 4. Преобразование Фурье функции вейвлета.

Рекомендуем скачать другие рефераты по теме: контрольные работы 8 класс, реферат на тему современные.



Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки